Shrinkage Method
subset selection은 불필요한 feature를 제거하여 모델의 성능을 향상하지만, 자칫 필요한 변수까지 제거할 수도 있다.
따라서 모든 feature를 이용하는 대신 regularization항을 추가하여 계수들이 0에 가깝도록 강제하는 Shrinkage Method에 대해 공부할 것이다.
대표적인 방법으로는 Ridge regression과 Lasso가 있다.
Ridge regression

Ridge regression은 다음과 같이 일반적인 선형 회귀 RSS에 계수들의 제곱합(l2 norm)에 대한 penalty term을 추가로 더하는 것이다.
\(\lambda\)가 크면 \(\beta\)가 작아져 분산이 작아지지만 bias가 커질 수 있다.
반면 \(\lambda\)가 작으면 \(\beta\)가 커져 분산이 커지고 bias가 작아진다.
추가로 \(\beta_0\)에 대해서는 shrinkage 시키지 않는다.
중심같은 느낌이다.
Coefficient

- 왼쪽 graph: \(\lambda\)가 증가할 수록 coefficient의 값들이 작아진다. coefficient를 세부적으로 보면 어떤 것은 늘어나는 것도 있는데 그 이유는 전체적인 합으로 보는 것이기 때문에 어떤 coefficient는 늘어날지라도 다른 coefficient들이 감소해서 전체적으로는 작아지는 것이다.
여기서 눈여겨 볼점이 coefficient이 0에 가까워지지 완전히 딱 0이 되지 않는다.
- 오른쪽 graph: 분자가 ridge regression을 했을 때 coefficient이고 분모는 일반적인(정규항 없는) 선형 회귀 coefficient이다. 따라서 두 값을 비교하여 1에 가까울수록 두 값이 비슷한 것이기 때문에 \(\lambda\)는 0에 가까운 것이다. 따라서 이 그래프는 오른쪽으로 갈수록 \(\lambda\)의 값이 작아지는 것이고 그에 따라 coefficient는 점점 커진다.
Scaling of predictors

scale에 따라 값이 달라질 수 있어 다음과 같이 standardization을 한다.
The Bias-Variance tradeoff

\(\lambda\)가 커질수록 bias(검은색)가 커지고 variance(녹색)가 작아지는 trade-off 관계에 있다.
이 두개가 더해진 것이 mse(빨간색)이고 적당한 \(\lambda\) 값에서 mse 최소가 된다.
따라서 \(\lambda\)는 너무 작아도 커도 안된다.
Lasso

Lasso는 일반적인 선형 회귀의 RSS에 계수들의 절댓값인 l1 norm을 더하여 coefficient를 학습하는 것을 말한다.
대부분의 내용은 위에서 설명한 ridge regression과 동일하다.
단, Lasso는 일부 계수가 정확히 0이 되게 할 수 있다. 이는 feature selection을 하는 효과도 가져올 수 있다.
Coefficient

Ridge regression때와 동일하게 해석할 수 있다.
단, 여기서 차이는 \(\lambda\)가 무한히 커지면 coefficient가 0이 될 수도 있다는 점이다.
따라서, Lasso를 이용하면 더 sparse한 모델이 형성된다.
이는 variance를 낮추지만 bias를 올릴 수도 있다.
이런 차이를 가지는 이유는 제약식을 자세하게 살펴보면 알 수 있다.
Why Lasso prefers sparse models?
- Lasso


Lasso는 다음과 같이 마름모꼴의 제약영역을 갖는다.
RSS가 동일한 값을 갖는 지점은 타원 형태를 이루고 이 타원과 제약영역이 접하는, 만나는 부분을 찾는다.
여러 만날 수있는 부분 중 마름모의 경우 모서리(\(\beta\)의 값이 0인)에서 만날 확률이 높다.
모서리에서 만날 경우 일부 coefficient는 정확히 0이 된다.
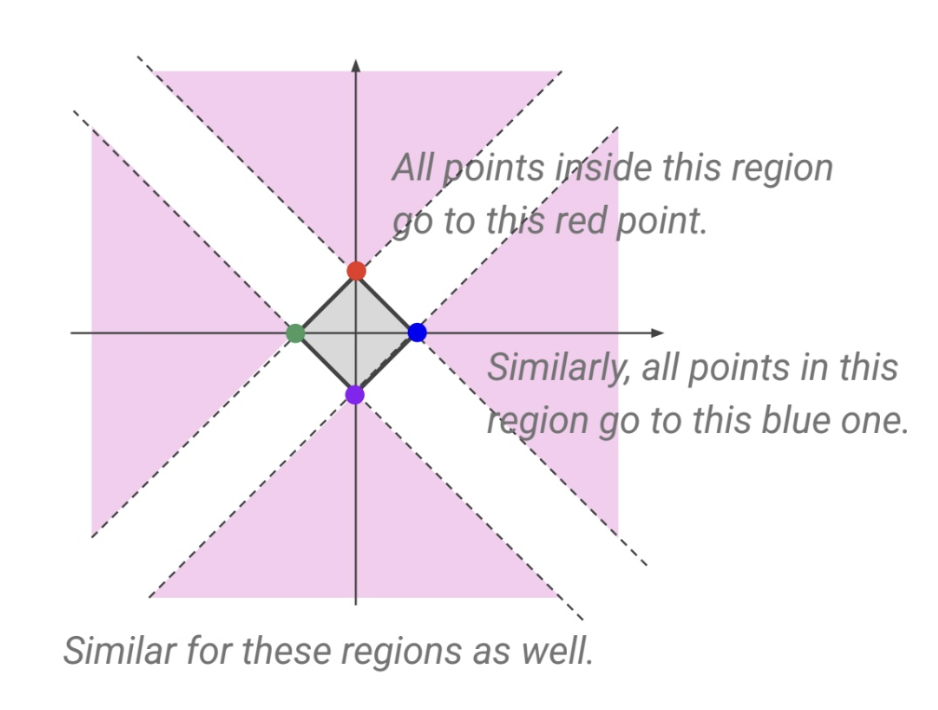
이 그림은 분홍색 region에 위치할 경우 모두 마름모의 모서리로 가는 것을 알 수있다.
이런점때문에 coefficient가 0이 될 확률이 높아진다.
- Ridge
반면 Ridge의 경우 제약 영역이 원, 구의 형태를 가진다.
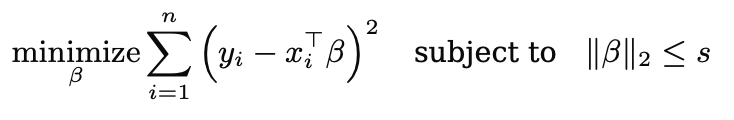

원의 경계는 매끄러운 곡선이라 축과 정렬된 지점(모서리와 같이 \(\beta\)가 0인)에서 만날 확률이 상대적으로 낮다.
이러한 이유 때문에 Ridge는 정확히 0이 되는 coefficient가 없는 것이다.
그럼 어떤 방법이 모델을 더 잘 만드는 것일까?
어떤 방법이 더 우세하다고 할 수는 없지만 true model의 predictors가 원래 적다면(sparse model) Lasso가 더 잘 모델링한다.
하지만 response와 관련된 predictors의 개수는 미리 알 수 없기 때문에 Cross-validation을 사용하여 어떤 방법이 좋은지 판단할 수 있다.

점선이 ridge일 때고 실선이 lasso일 때다.
black이 bias, green이 variance, purple이 MSE
오른쪽 그래프를 보면 \(R^2\) 에 대한 mse, bias, variance를 본 것이다.
\(R^2\) 이 증가한다는 것은 \(\lambda\)의 값이 작아지는 것이다.
그 이유는 제약이 없어지기 때문에 더 잘 예측할 것이기 때문에 표현력이 높아진다.
따라서 그래프를 보면 variance(green)가 증가하고 bias(black)가 감소한다.
Ridge와 Lasso를 비교하면 true model이 sparse 하기 때문에 Lasso일 때가 성능이 더 좋다.
(여기서 true model이 sparse model인건 predefine 한 거다)
Select the Tuning Parameter
\(\lambda\)의 크기에 따라 모델이 사용하는 feature의 개수가 달라지고 coefficient의 값도 달라진다.
\(\lambda\)는 cross-validation과정을 통해 select 된다.

보는 것처럼 \(\lambda\)가 지나치게 커지면 모델이 너무 sparse 해져 예측을 잘 못할 수 있다.
따라서 적당한 \(\lambda\)를 선택해야 한다.
오른쪽 그래프는 \(\lambda\)가 커질수록 coefficient가 전체적으로 감소하고 처음부터 영향이 적었던 feature는 coefficient가 계속 작다.

이 그래프도 동일하다.
x축은 커질수록 \(\lambda\)가 작아지는 것이다.
따라서 coefficient를 봐도 왼쪽으로 올수록 0으로 되는 coefficient가 생기는 것이다.