train error와 test error의 관계는 어떻게 될까?
모델을 만들었을 때, 최종 목표는 test error를 줄이는 것이다.
학습할 때는 test dataset을 볼 수 없으며 이용해서도 안된다.
그럼 어떻게 test error를 낮추고 확인할 수 있을까?
오늘 공부할 내용은 test error를 추정하고 이를 낮출 수 있는 방법이다.
Training Error vs Test Error
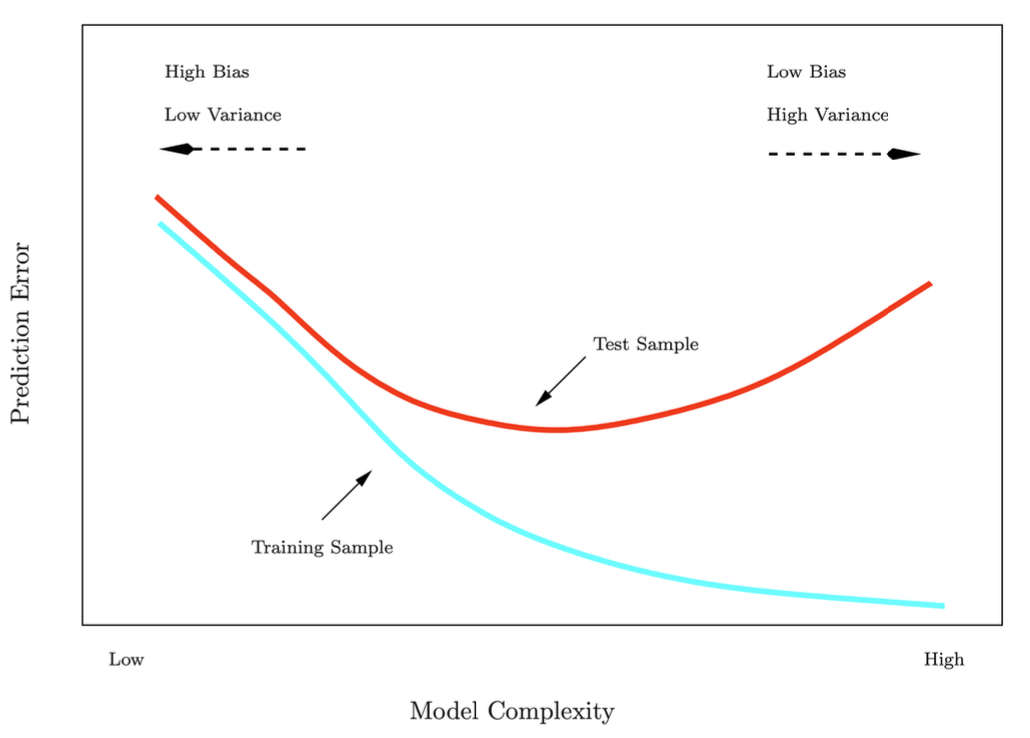
train dataset과 test dataset은 기본적으로 같은 분포고 특별히 뭐가 어렵고 쉬운 것은 아니다.
test error는 학습 때 사용하지 않은 새로운 관측치에 대해 예측하여 발생하는 error이다.
반면에 train error는 train할 때 본 관측치에 대해 발생하는 error이다.
단지, 학습할 때 보지 못한 test dataset을 보고 모델이 예측하는 것이기 때문에 error를 underestimate 한다.
사실 error를 추정하여 줄이는 가장 이상적인 방법은 대규모 데이터셋을 구하는 것이다.
하지만 현실에서는 쉽지 않다.
현실적으로는 Cross-validation이나 hold-out 그리고 \(C_p\)statistic/AIC/BIC을 이용한다.
Validation Set approach
랜덤하게 training set과 validation set으로 나눠 모델을 학습하고 error를 추정한다.
validation-set error가 test error의 추정치인것이다.

그러나 이 방법은 높은 변동성을 가지고 있다.
데이터 분할 과정이 임의적이기 때문에, 어떤 샘플이 훈련 세트로 어떤 샘플이 검증 세트로 배정되는지에 따라 검증 오차가 크게 달라질 수 있다.
즉, 한번의 분할 결과만으로는 모델의 일반화 성능을 안정적으로 추정하기 어렵다.

보는 것처럼 어떻게 split하냐에 따라 변동성이 너무 크다.
또한 원래 훈련하기 위해 쓰려는 데이터의 일부를 split하여 validation set으로 쓰므로 결과적으로 학습데이터의 양이 줄어든다.
이는 validation set으로 추정한 error가 실제 값보다 overestimate될 가능성이 있다.
이런 단점을 보완하고자하는 K-fold Cross validation 방법을 공부해보도록 하자.
K-fold Cross validation
전체 데이터 n개를 K개의 fold로 나눕니다.
각 fold는 겹치지 않는 서로 다른 관측치들의 집합이며, fold의 크기는 보통 비슷하게 맞춘다.
폴드\(k\) 1개를 validation set으로 두고, 나머지 \(k-1\)개의 폴드를 training set으로 사용한다.

K개에 대해 각각 반복하고 모든 폴드에 대한 error를 평균내서, 최종적으로 모델의 test error를 추정한다.
$$ \textbf{CV}_{(K)} = \sum_{k=1}^{K} \frac{n_k}{n} \text{MSE}_k $$
\(n_k\)는 \(k\) fold에 있는 데이터 개수이다.
Leave-one out cross-validation(LOOCV)
LOOCV는 K-폴드의 특수한 형태로 \(K=n\)일 때다.
즉, 각 관측치 1개가 validation에 사용되고 나머지는 n-1은 train하는데에 사용한다.

이럴 경우, 모델이 거의 모든 데이터 셋에 대해 학습을 할 수 있기 때문에 bias가 낮아진다.
하지만 데이터 1개(validation set)로 error를 추정하고 1개의 데이터셋에 민감하게 반응할 것이기 때문에 variance가 크다.
이 경우 n번 모델을 학습해야하는데 데이터가 큰 경우 계산비용이 만만치 않을 수 있습니다.
K-fold(k=10)과 LOOCV 비교

LOOCV는 무조건 n으로 나눠야하므로 무작위 분할이 없는 반면 10-fold는 분할하는 것 자체가 랜덤이다.
따라서 어떻게 분할하냐에 따라 평균 MSE값이 달라진다.
LOOCV는 무작위 분할 측면에서 분할이 고정돼있기 때문에 변동성이 없다 할 수있지만 error estimate 측면에서는 각 1개의 데이터로 검증하기 때문에 민감할 수 있다.
이런 bias-variance tradeoff를 고려할 때 K를 5또는 10으로 해도 적절한 균형을 이룰 수 있어, 모델 성능을 안정적으로 추정하기 좋다.
test error를 추정하기 위해 Cross-validation 값을 사용하기 때문에 이 Cross-validation(CV)이 얼마나 안정적인지를 판단해야한다.
그 방법으로 \(CV_k\)의 standard deviation을 구한다.
$$ \widehat{\text{SE}} (\text{CV}_K) = \sqrt{ \frac{1}{K} \sum_{k=1}^{K} \frac{(\text{Err}_k - \text{CV}_K)^2}{K - 1} } $$
이 방법은 꽤나 쓸모있지만 fold간 예측 오차들이 완전히 독립적이지 않기 때문에 완전히 타당하지는 않다.
그래도 실무적 관점에서는 비교적 간단하면서도 유용하게 분산 정도를 가늠하는 근거가 된다.
feature selecting 과정에서 Cross-validation을 이용하는 것을 보겠다.
예를 들어 1000개의 predictors가 있고 50개의 samples가 있다고하자.
이때 class label과 상관관계가 상위 100개인 predictors에 대해 고르고 이것으로 모델을 만들었다.
이후 Cross-validation을 진행한다면 올바른 과정일까?
당연히 아니다.
이미 feature를 고르는 과정에서 dataset에 대해 봤기 때문이다.
feature를 select하는 과정도 모델을 만드는 과정이므로 cross-validation을 하면서 같이 결정해야한다.
'Machine learning & Deep learning' 카테고리의 다른 글
| [Machine learning] Bootstrap에 대해 알아보기 (0) | 2025.03.29 |
|---|---|
| [Machine learning] Linear regression, Logistic regression code 구현중 모르거나 헷갈렸던 code 정리 (0) | 2025.03.26 |
| [Machine learning] ML 3주차 공부(Classification? Discriminant Analysis) (0) | 2025.03.21 |
| [Machine learning] Classification? Logistic Regression? 에 대한 완전 정리 (1) | 2025.03.13 |
| [Machine learning] ML 2주차 공부(Linear Regression의 모든 것 2) (0) | 2025.03.11 |