Tree-based Methods
분류와 회귀 작업 모두에 사용 가능하며, 입력공간을 재귀적으로 분할하여 단순한 영역으로 나눈다.
이 방법은 시각적으로 이해가 쉽고, 해석력 높은 모델을 만들 수 있다.
단, 정교한 supervised model에 비해 예측 정확도 면에서 성능이 떨어진다.
이 것을 해결하기 위한 방법으로 bagging, random forests, boosting이 있다.
이 내용에 대해서는 다음에 공부하도록 하겠다.
Tree-based model에 Decision tree가 있으며, 오늘은 이 내용에 대해 알아보도록 하겠다.
Decision Trees

Decision Tree는 이름 자체에서도 알 수 있듯이 Tree-based model이다.
따라서, regression과 classification을 둘 다 할 수 있다.
먼저 Decision Tree를 이용하여 Hitters data set을 이용하여 regression 하는 것을 알아보도록 하겠다.
target은 baseball player's Salary이다.
경력이 얼마나 됬는지(Years)와 타율이 어떻게 되는지(Hits)를 predictor로 이용한다.


왼쪽은 Hitters data set이고 오른쪽은 이 data set을 이용하여 decision regression을 한 것이다.
먼저, Years에 대해 4.5 기준으로 나누고 이후에 Hits에 대하여 117.5 기준으로 나눈다.
그러면 3가지 영역이 나오고 predictor space를 다음과 같이 표현할 수 있다.


이렇게 모델링한 Tree에 대해 Terminology를 정리해보면
각각의 영역 \(R_1, R_2, R_3\)을 terminal nodes라 한다.
tree는 위에서 아래로 upside down형태를 가지며, 각각 분기하는 지점을 internal node라 한다.
결과에 대해 해석해 보면
Years를 통해 가장 먼저 분기하기 때문에 Salary에 있어 가장 중요한 factor라고 할 수 있다.
특히, 경력이 낮은 영역을 보면 Hit에 따른 연봉차이가 별로 없어 보인다.
그러나 경력이 5+years인 경우 Hit가 클수록 Salary가 올라가는 양상을 볼 수 있다.
Tree building process를 자세히 살펴보면
어떻게 얼마나 나눌까? 가 핵심이다.
How to make a Tree?
먼저 어떻게 나눌까에 대한 답변은
당연히 regression이니깐 \(RSS\)가 작아지는 방향으로 나눠야 한다.
이 부분에 대해 자세히 살펴보면

\(R_j\)는 각 영역을 나타내며 \(j\)는 영역의 index, \(J\)는 개수, \(i\)는 region에 있는 데이터를 나타낸다.
Decision tree에서는 각 영역에 대해 예측 값을 그 영역에 속한 \(y\)들의 평균으로 한다.
따라서 임의로 나눴을 때(\(J\) 개의 영역이 생김) 각 영역의 평균값과 관측값들의 오차를 구해 \(RSS\)를 계산한다.
어떻게 영역을 나누냐에 따라 영역에 들어가는 \(y\) 값들이 달라지므로 \(RSS\) 값들이 달라진다.
어떻게 나눌까에 대한 답은 했으므로 얼마나 나눌까에 대한 대답을 해보면
당연히 \(RSS\) 값이 최소가 될 때까지 나누면 좋을 것이다.
그때가 언제인지를 생각해 보면 \(J\) 개의 영역에 대해 각 영역의 평균이 거기 속한 관측값이 돼야 된다.
즉, 모든 Data에 대해 Region을 생성하는 것이다.
이렇게 되면 뭐가 문제일까?
다른 데이터에 대한 일반화 능력이 떨어지는 Overfitting이 발생한다.
따라서 무작정 \(RSS\)를 작게만 하면 안 되는 것이다.
이 문제를 잠깐 뒤로 제쳐두고 그럼 \(RSS\)를 연산하는 측면에서 보면 모든 \(J\) 개의 영역으로 나눠 계산을 할 수 있을까?
당연히 불가능하다.
그렇기 때문에 top-down 형식으로 각 단계에서 바로 지금 가장 좋은 분할을 선택하는 Greedy 한 방법을 이용한다.
Baseball player's Salary와 관한 문제로 돌아와서
tree를 만드는 과정을 생각해 보면

j는 feature index이고 s는 cutpoint value이다.
여기서는 j=1(years)에 대해 s=4.5일 때 \(RSS\)가 최소가 되는 것이다.
영역을 select 하는 과정에서 이론적으로는 region의 shape은 아무거나 돼도 상관없다.
그러나 단순화를 위해 주로 box형태(축에 평행한 직사각형)를 region으로 선택한다.
아까 Overfitting 문제로 다시 돌아와서
해결하는 방법에 대해 알아보겠다.
극단적으로 생각했을 때 모든 데이터에 대해 영역을 형성하는 것이 Overfitting을 일으켰다.
그럼 variance를 낮추면 되는 것이고 region의 개수를 줄이면 된다.
Pruning a Tree
이 방법을 가지치기 Pruning a Tree라 한다.
Pruning a Tree를 할 때도 고려해야 할 점이 있다.
언제 Pruning을 할까?
가장 단순하게 생각해서 \(RSS\)를 기준으로 정한다고 해보자.
region의 개수가 증가함에 따라 \(RSS\)가 감소할 텐데, \(RSS\) 감소량의 threshold를 걸어놓아 그 기준보다 적다면 split을 멈추는 것이다.
이 방법의 문제점이 무엇일까?
예를 들어 2>3번째 \(RSS\) 감소량이 적어 2번째에서 멈췄을 경우에 대해 보자.
만약 4>5번째로 갈 때 \(RSS\) 감소량이 엄청 많았다면 어떻게 될까?
당연히 2번째에서 split을 멈춘 건 잘못된 일이다.
즉, 너무 short-sighted 한 방법이다.
Cost complexity pruning
따라서 Cost complexity pruning방법을 사용한다.
이 방법은 \(RSS\) term에 영역의 개수가 많아지는 것에 penalty를 주는 term을 더하는 것이다.

\(\alpha\)를 임의로 정하여 Tree의 예측 성능과 복잡도 사이의 균형을 조절하는 방식이다.
Ridge regression과 Lasso의 regularization term과 비슷하다고 생각하면 된다.
\(\alpha\)가 작을수록 복잡한 tree를 허용한다는 것이다.(\(T\)의 크기가 커지니깐)
\(\alpha\)가 클수록 간단한 tree를 선호한다는 것을 알 수 있다.
그럼 최적의 \(\alpha\)는 어떻게 구할까?
여러 \(\alpha\)에 대해 Cross-validation을 수행하고 error가 가장 작은 \(\alpha\)를 선택한다.
Regression tree algorithm Summary
- 최소한의 관측치가 남을 때까지 recursive binary splitting을 계속한다. (top-down greedy splitting)
- Cost complexity pruning을 사용하여 step 1에서 만든 tree를 기반으로 여러 개의 subtree를 생성한다.(\(\alpha\)에 따라 다른 값)
- K-fold cross validation을 이용하여 \(\alpha\)를 선택한다.
- 최종 생성한 tree를 반환한다.
Regression Tree on Hitter data
다시 아까 예제로 돌아와서 tree를 만드는 과정을 살펴보겠다.
먼저 1번째 step대로 greedy splitting으로 unpruned tree를 만든다.


unpruned tree은 다음과 같이 12개의 region으로 구성돼 있다.
2번째 step으로 넘어와서 Cost complexity pruning을 사용하여 \(\alpha\)에 따른 subtree를 형성한다.
\(\alpha\)의 크기에 따라 Tree size가 변하는 것이다.
cross-validation error를 통해 optimal 한 \(\alpha\)를 찾아 그때의 tree로 결정한다.
그래프를 통해 보면 Tree size가 2와 4 사이 일 때 validation error가 가장 최소이다.
단, 여기서 주의해야 할 점은 Test error를 보고 10에서 가장 작다!라고 판단하면 안 된다.
왜냐하면 우리는 test data set에 대해 알 수없기 때문이다.
unpruned tree를 통해 12개의 region으로 정했지만 Cost complexity pruning을 하여 3개의 region을 가질 때가 optimal 한 것이라고 결론을 낼 수 있다.
Classification trees
사실 regression tree와 quantitative response를 예측하는 것을 제외하곤 매우 비슷하다.
또한 regression tree에서는 예측값으로 평균을 사용했다면 Classification tree에서는 가장 많이 나타난 class를 예측 값으로 사용한다.
classification tree를 만드는 과정에서도 \(RSS\)와 같은 error를 계산하는 기준이 있는데
Classification Error rate

확률 \(\hat {p}_{mk}\)은 \(m\) 번 노드(\(m\) 번 영역)에서 \(k\) 번 클래스의 비율을 말한다.
즉, 가장 흔한 class의 비율이고 \(E\)를 가장 흔한 class의 비율을 제외한 나머지로 정의한다.
하지만 이 방법은 tree를 생성하는데 충분하지 않아 실전에서 잘 사용하지 않는다.
Gini index and Cross-entropy
Gini index
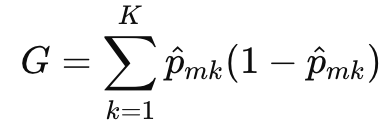
\(k\) class인 경우와 그 외의 경우를 곱해 섞임 정도를 나타내는 값이다.
여러 class의 이러한 섞임 정도를 모두 더하면 전체적인 impurity를 측정할 수 있다.(sum을 k class에 대해 하는 것)
gini index가 작을수록 불순도가 낮다.
불순도 낮다는 것은 특정 class가 우세하다는 뜻인데 그것은 결국 잘 분류가 돼있다는 뜻이다.
Cross-entropy

gini index와 비슷하게 node impurity를 계산한다.
정보이론에서 유래된 개념이다.
여러 class에 확률이 분산되어 있으면 엔트로피가 큰 상태이고 class가 한 곳에 몰려있으면 entropy가 작은 상태이며 우리가 달성하고자 하는 목표이다.
실전에서 가장 많이 쓰이는데 그 이유는 \(log\) term으로 되어있기 때문에 gradient가 잘 정의된다.
Classification Tree on heart data
target은 yes or no이고 13개의 predictor가 있는 문제이다.
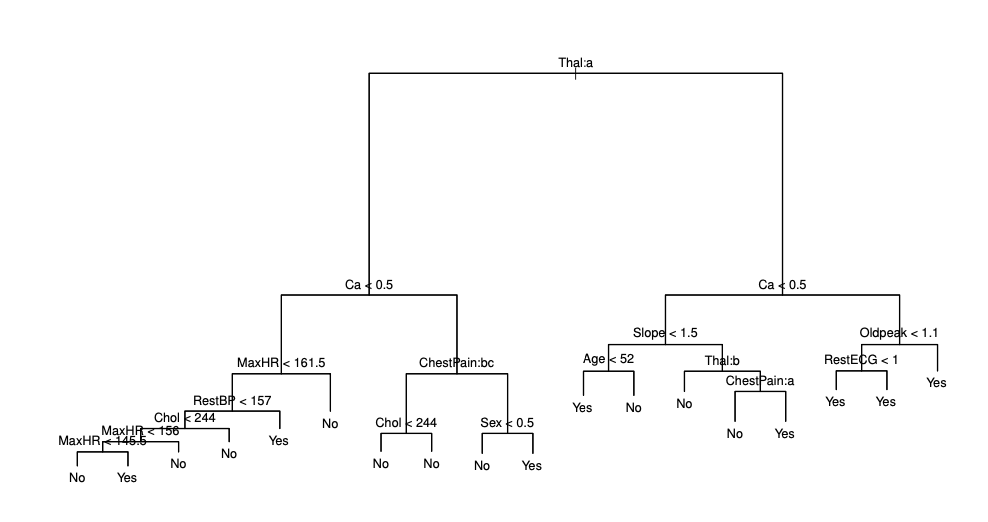
step 1에서 말했던 것처럼 18개의 영역을 가진 Unpruned tree를 만든다.
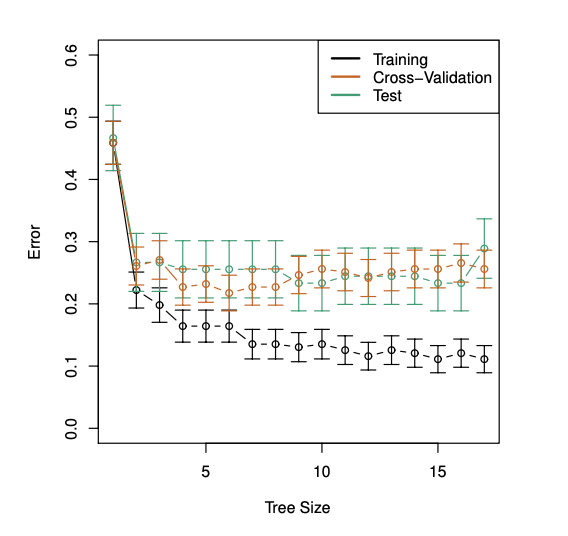

Step2에서처럼 정규항을 넣고 cross-validation을 통해 error가 가장 낮은 tree size를 고른다.
tree size가 6일 때 가장 작은 cross validation error를 가지는 것을 확인할 수 있다.
Advantages and Disadvantages of Trees
- easier to explain than linear regression(+)
- more closely mirror human decision making(+)
- can be displayed graphically and easily interpreted(+)
- easily handle qualitive predictors don't need to create dummy variable(+)
- low predictive accuracy(-)
- non-robust(-)
Linear model vs Decision Tree

보는 것처럼 true 영역이 선형이면 linear model이 더 fit 하고 비선형이면 Decision tree가 더 fit 하다.
'Machine learning & Deep learning' 카테고리의 다른 글
| [Machine learning] 머신러닝에서 사용하는 통계적 오차 측정 지표의 차이 알아보기 (0) | 2025.04.17 |
|---|---|
| [Machine learning] Confounding Effect, Interaction Term, MultiCollinearity의 차이 (0) | 2025.04.14 |
| [Machine learning] How to select optimal model(feature selection, one-standard-error rule) (0) | 2025.04.05 |
| [Machine learning] Lasso와 Ridge regression 중 어떤 것을 사용?? (0) | 2025.04.04 |
| [Machine learning] Bootstrap에 대해 알아보기 (0) | 2025.03.29 |