모델의 feature의 개수가 증가하면 Accuracy가 높아진다.
그러나 모델이 복잡해지므로 interpretability가 낮아지고 coefficient의 분산이 커지므로 새로운 값에 대해 예측이 불안정하다.
이런 점 때문에 단순히 feature의 개수만 늘려서 모델의 성능이 좋아진다고 판단하면 안된다.
feature를 어떻게 고를 것이며 몇개를 골라야할지에 대해 공부해보도록 하겠다.
Best Subset Selection
모든 조합을 전부 살펴보는 것이다.
1단계: Null Model(\(\mathcal{M}_0\)) 설정
아무 predictor도 포함하지 않은 모델로 모든 관측값에 대해 평균값으로 예측하는 모델이다.
2단계:feature 개수별 후보 모델 탐색
변수가 \(p\)개있고 그 중 \(k\)개에 대한 모든 조합을 확인하는 것이다.
feature가 1,2,...,p개일 때를 모두 보는 것이다.
한 \(k\)에 대해 \(\binom{p}{k} = \frac{p!}{k!(p-k)!}\)을 계산한다.
이후 각 \(k\)에 대해 가장 좋은 모델 \(\mathcal{M}_k\)를 선택한다.
좋은 모델의 기준은 보통 각 \(k\)끼리 \(RSS\)이 작거나 \(R^2\)이 큰 모델을 고른다.
3단계: 최종 모델 선택
각 변수 개수에 대해 가장 좋은 모델을 뽑고, 그 중 진짜 베스트를 고르는 구조이다.
이 때 사용하는 기준으로는 Cp,AIC,BIC,Adjusted \(R^2\)등을 기준으로 한다.
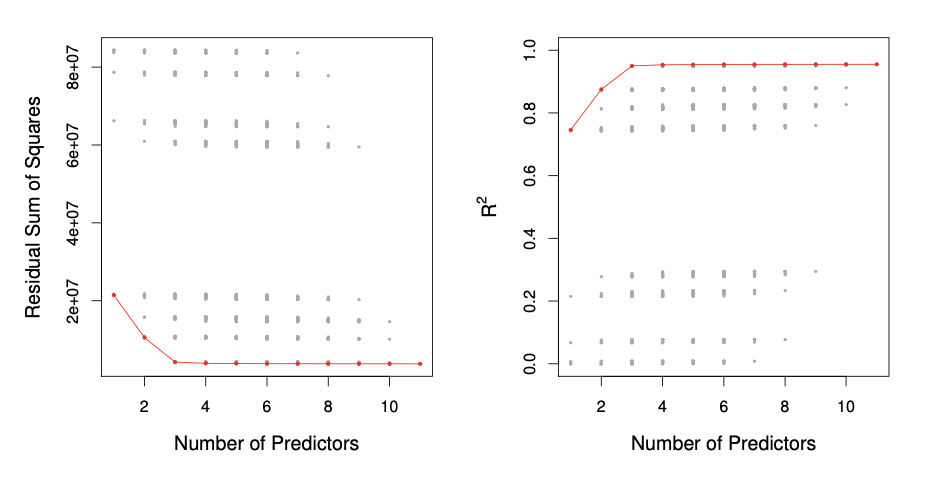
빨간 선은 각 predictor에 대해 가장 좋은 성능일 때를 이은 것이다.
Stepwise Selection
Best Subset Selection 방법은 \(2^p\)조합으로 computational issue가 있다.
따라서, 전체 조합을 보지않고 일부 경로만 탐색하는 Stepwise selection방법을 많이 사용한다.
Stepwise Selection에는 forward와 backward 두가지 방법이 있다.
Foward Stepwise Selection
1단계
subset selection과 동일하게 \(\mathcal{M}_0\)에서 시작한다.
2단계
\(k=0,1,...,p-1\)동안 추가했을 때 성능 향상이 가장 큰 변수를 선택한다.(추가했던 feature는 변하지 않는다.)
모든 변수를 다 넣어 총 \(p+1\)개의 모델을 만든다.
당연히 \(\mathcal{M}_p\)가 train dataset에 대해서 가장 성능이 좋을 것이다.(RSS가 낮아지게 feature를 계속 추가했으므로)
따라서 모델을 generalize시키기 위해 3단계를 진행한다.
3단계
\(\mathcal{M}_0,\mathcal{M}_1,....,\mathcal{M}_p\)중에서 Cp, AIC, BIC, Adjusted \(R^2\)을 기준으로 최종 모델을 선택한다.
이 metric을 써도 되고 cross-validation을 통해 test prediction을 추정하여 best model을 선택해도된다.
이 방법은 계산량이 \(p^2\)으로 줄었다는 장점이 있지만 greedy한 방법으로 global 해를 찾지 못한다.

3개의 feature까지는 동일한데 4번째부터 best subset은 cards가 들어온 반면 Forward stepwise는 rating이 그대로 있다.
즉, Forward stepwise는 한 번 고른 선택에 묶이게 돼 global한 해를 찾을 수 없다.
Backward Stepwise Selection
1단계
모든 \(p\)개의 feature를 포함한 \(\mathcal{M}_k\)에서 시작한다.
2단계
\(k=p,p-1,...,2,1\)동안 feature 하나 씩 제거하여 모든 모델을 고려한다.
3단계
\(\mathcal{M}_0,\mathcal{M}_1,....,\mathcal{M}_p\)중에서 Cp, AIC, BIC, Adjusted \(R^2\)을 기준으로 최종 모델을 선택한다.
단, backward selection일 경우 full model에서 시작하므로 sample의 개수 \(n\)이 항상 feature의 개수 \(p\)보다 항상 커야한다.
하지만 forward selection일 경우 \(n<p\)여도 이용할 수 있다.
Choosing the Optimal Model
\(R^2\)또는 \(Rss\)을 모델 선택의 기준으로 삼는다면 문제가 발생한다.
feature를 늘릴수록 train data에 대해 과하게 학습하여 \(R^2\)또는 \(Rss\)에서는 좋은 성능을 가진다고 해석된다.
하지만 실제에서는 train data에 대해서 판단을 하기 때문에 위와같은 방법으로 optimal model을 선택하는 것은 문제가 있다.
따라서 새로운 방법에 대해 알아보겠다.
test error를 추정하는 방법
- 간접적 추정
모델 복잡도에 따른 penalty를 추가하여 예상 test error를 보정한다.
feature의 개수가 많을 수록 penalty를 주는 것이다.
대표적인 방법으로 \(C_p, AIC, BIC, Adjusted R^2\)이 있다.
- 직접적 추정
모델의 예측 성능을 직접적으로 test set에서 측정하는 것이 가장 확실하지만 이렇게는 하기 힘드므로 Cross-validation방법을 주로 쓴다.
Mallow's \(C_p\)

모델의 복잡도(feature의 개수 d)를 고려한 기준이다.
d가 늘어날 수록(feature의 개수 증가) RSS의 값은 작아진다.
반면 \(2d \hat{\sigma}^2\)가 증가하여 전체 \(C_p\)는 다시 커질 수 있다.
따라서 단순히 \(RSS\)값으로 성능을 판단하기 보다는 feature의 개수를 반영하여 성능을 판단하여 \(C_p\)가 작을 수록 성능과 단순함을 모두 만족하는 모델로 간주할 수 있다.
즉, feature의 개수에 따른 penalty를 준것으로 개수가 많을 수록 \(C_p\)값이 크다.
\(C_p\)값이 작아야 좋은 것이다.
BIC
BIC는 \(C_p\)와 비슷하다.
단지 \(2d \hat{\sigma}^2\)를 \(log(n)d \hat{\sigma}^2\)로 바꿨을 뿐이다.
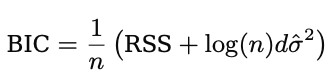
BIC는 \(C_p\)보다 feature가 더 많은 모델들에 큰 penalty를 준다.
수식을 보면 \(log(n)\)가 2보다 큰 경우는 \(n>7\)인 경우기 때문이다.
n은 통상적으로 큰 숫자일 경우가 많다.
따라서 feature의 개수가 많은 모델에 대해 BIC의 값이 \(C_p\)보다 크다.
즉, feature의 개수가 많아지는 것에 대해 더 제약하는 것이다.

그래프를 봐도 \(C_p\)는 feature가 6개일때가 opimal인데 feature의 개수에 대해 더 엄격한 BIC는 4개일때 optimal하다고 판단한다.
AIC

L은 모델의 likelihood이고 d는 모델의 feature 개수이다.
모델의 설명력과 복잡도 사이의 균형을 맞춘것이다.
Adjusted \(R^2\)
일반적인 \(R^2\)은 feature의 개수가 증가할 수록 커진다.
이는 과적합을 유도할 수 있다.
Adjusted \(R^2\)은 변수 증가에 대해 penalty를 부여하기 때문에 feature의 개수가 증가한다고 커지는 것은 아니다.
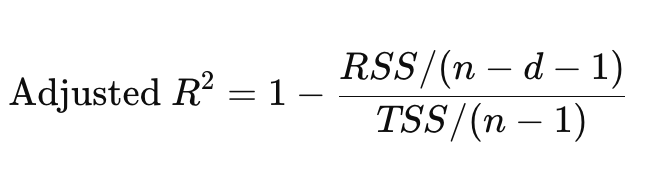
식을 보면 \(d\)가 커지면 분모의 항이 커지므로 전체 \(R^2\)은 작아진다.
따라서, feature의 개수가 늘어나는 것에 대해 penalty부여한다.
Test error의 간접적 추정과 직접적 추정
그냥 Cross-validation을 이용해서 test error를 추정하면 되지 왜 귀찮게 BIC,\(C_p\)값을 구하는지 이해가 안 될 수 있다.
일단, 각각 둘은 성능상 비슷하다.
직접적으로 추정하는게 당연히 더 정확할 가능성이 높고 간접적 추정도 이에 못지 않게 잘한다.
그러나 test error를 직접 추정한다는 것은 그만큼 inference time이 있다는 것이다.
반면 간접적으로 추정할 경우 train error에 파라미터만 추가해서 계산만 하면된다.
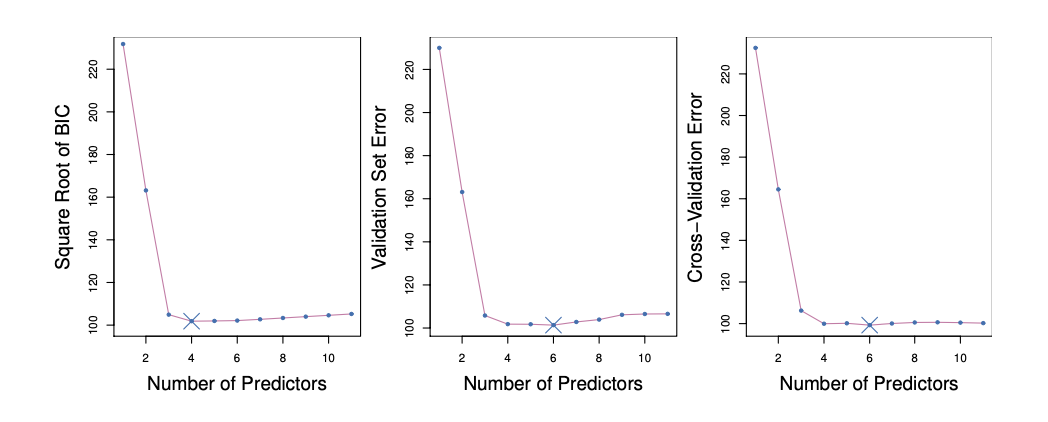
그럼 이제 optimal model을 어떻게 고를까?
How to choose optimal model
우리는 one-standard-error rule을 통해 모델링을 해야한다.
train error의 추정값이 가장 작은 모델을 바로 고르지 않고 그 최저점에서 표준오차 1개 이내에 있는 가장 단순한 모델을 고르는 것이다.
예를들어 feature가 10개일때 train error의 추정값이 최저값일때, 그 error값의 표준오차 1개에 해당하는 train error값을 보고 feature가 7개일때도 그 error값이 나왔다면 10개말고 7개로 정한다는 것이다.
simplest model을 선택하는 것이다.
모델을 평가할때는 단순히 가장 좋은 성능이 아니라, 복잡도 대비 성능 균형, 안정성, 해석력 등을 고려해야한다.