Bootstrap
Bootstrap은 resampling 기법으로, 이미 확보된 하나의 데이터셋에서 복수의 새로운 표본을 생성하여 추정량(모델의 파라미터)의 uncertainty를 평가하는 방법이다.
단, 여기서 sampling은 with replacement(복원 추출)로 이뤄진다.
resampling을 통해서 예를 들어 100개의 데이터만 가지고도 100+개의 데이터로 추정한 성능을 내는 것이다.
bootstrap을 통해 coefficient의 standard error나 confidence interval를 추정할 수 있다.
간단한 예시를 들어보겠다.
두 금융자산 \(X, Y\)의 수익률이 있고, 한정된 자금을 \(\alpha\)만큼은 \(X\)에, 나머지\(1-\alpha\)만큼은 \(Y\)에 투자한다고 한다.
이때, 투자 위험(분산) \(Var(\alpha X+(1-\alpha)Y)\)를 최소화하는 \(\alpha\)를 찾는다 하자.
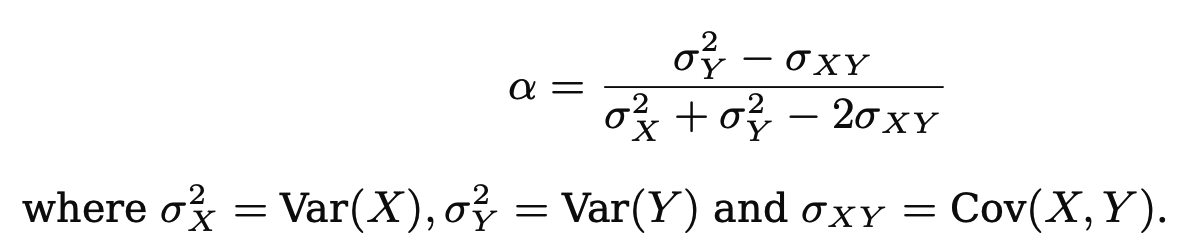
하지만 \(X\)와 \(Y\)에 대해 잘 알지 못하므로 추정을 해야한다.
이때 bootstrap을 사용하여 \(X\)와 \(Y\)의 분산과 공분산을 추정한다.
그럼 \(\alpha\)의 추정값을 다음과 같이 구할 수 있다.



총 4가지의 그래프에 대해 설명해 보면
- X, Y에 대해 resampling 해서 분산, 공분산을 추정하는 것이다.
- 진짜 실험을 k 번한 것이고
- 실험은 1번 했지만 복원추출하여 k개를 만들어냄
- bootstrap이 꽤 괜찮은 추정치를 제공할 수 있다는..

즉, 부트스트랩은 컴퓨터를 이용해서 새로운 데이터 set을 얻는 것처럼 흉내(mimic the process) 낼 수 있게 한다.
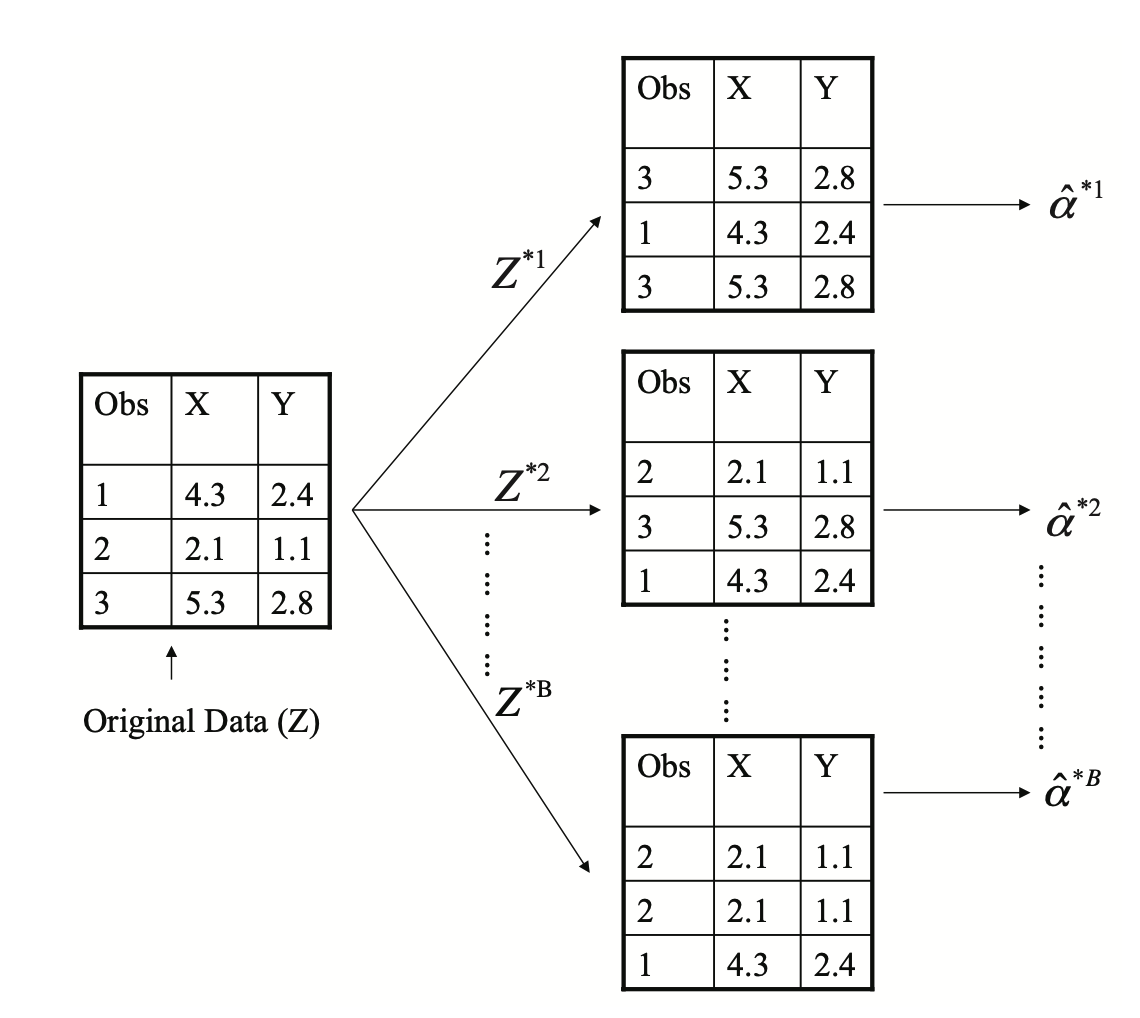
여기서 인지하고 있어야 하는 점은 with replacement(복원추출) 이기 때문에 중복된 값이 포함될 수 있다는 것이다.
그럼 시계열 데이터에서도 bootstrap을 적용할 수 있을까?
시계열 데이터는 시간에 따른 순서와 의존성이 중요하다.
따라서, 관측치를 무작위로 복원 추출하면 순서도 깨지고 시간적 구조도 무너진다.
대신, 시간을 block(연속된 관측값 묶음)으로 만들고 복원추출로 뽑아 붙여서 새로운 데이터셋을 구성할 수 있다.
그럼 K-fold validation처럼 train error를 추정하는 데에도 사용할 수 있을까?
데이터의 2/3가 겹치기 때문에 train dataset의 일부가 validation dataset이 될 수 있다.
따라서, error를 underestimate 하기 쉽다.
이 부분에 대해 조금 더 추가 설명을 해보면
어떤 데이터 1개가 한번도 안뽑힐 확률은 1-1/n이다.
이걸 n번 시행하면

즉, 이걸 좀 해석해보면 100개를 뽑아야하는데 100개가 63종류(100*2/3)의 데이터로 구성되는 것이다.
그러면 당연히 여기에는 중복이 생긴다.
이런 중복으로 인해 train error를 underestimate하는 것이다.
error를 prediction 하는 것은 웬만하면 K-fold validation으로 하는 게 나은 듯싶다.
error를 estimate 하고 싶으면 K-fold validation을 쓰고 변동성과 같은 uncertainty를 estimate 하고 싶으면 bootstrap을 쓰면 될 것 같다.