이번 metric learning에 대한 내용 정리는 서울대학교 이준석 교수님 강의를 바탕으로 제작되었습니다.
Metric learning
기존 supervised learning과는 다르게 data 간의 distance(=similarity)를 배우는 방법입니다.
데이터 간 서로 얼마나 비슷한 정도를 배우는 상대적인 개념으로 주관적인 개념입니다.
따라서 전통적인 Supervised learning으로는 이러한 관계를 파악하기 어렵습니다.
얼핏 보면 상대적인 관계를 학습하기 힘들겠다고 생각이 들 겁니다.
그러나 학습 시 label이 필요 없기 때문에 대규모의 데이터에 대해 쉽게 학습을 할 수 있다는 장점이 있습니다.
Metric learning 중 information retrieval에서 쓰이는 Learning to rank에 대해 알아보고 가장 많이 쓰이는 Triplet loss와 Contrastive learning에 대해 알아보겠습니다.
Learning to rank
Learning to rank의 종류에는 point-wise, pair-wise, list-wise가 있습니다.
point-wise는 query와 item에 대하여 수치적인 값으로 나타납니다.
pair-wise는 query에 대해 두 item의 순서 정보가 담겨있습니다. 이 순서를 맞추는 것을 목표로 합니다.
마지막으로 list-wise는 두 개 보다 많은 item에 대해 순서를 맞추는 것을 목표로 하는데 계산량이 많아 종종 해결하기 힘든 문제로 남습니다.
Learning to rank을 평가하기 위해 Normalized Discounted Cumulative Gain(NDCG)을 사용합니다.
$$ DCG_p = \sum_{i=1}^p \frac{rel_i}{\log_2(i+1)} $$
$$ DCG_p = \sum_{i=1}^p \frac{2^{rel_i} - 1}{\log_2(i+1)} $$
\(rel_i\) = 1 (i번째 결과가 실제로 관련 있을 때), \(rel_i\) = 0 (그렇지 않을 때)
첫 번째 수식을 살펴보면 총 p개의 순위를 맞추는 것입니다.
첫 번째 순위부터 p순위까지 앞쪽 순위를 맞출수록 더 높은 점수를 주기 위해 \(\log_2(i+1)\)로 나눕니다.
두 번째 수식은 \(rel_i\)의 값이 실수일 수도 있기 때문에 2의 제곱으로 표현합니다.
DCG를 normalize 한 값인 NDCG도 많이 이용하는데, 이 값은 DCG를 maximum possible DCG score로 나눠서 구합니다.
Triplet loss
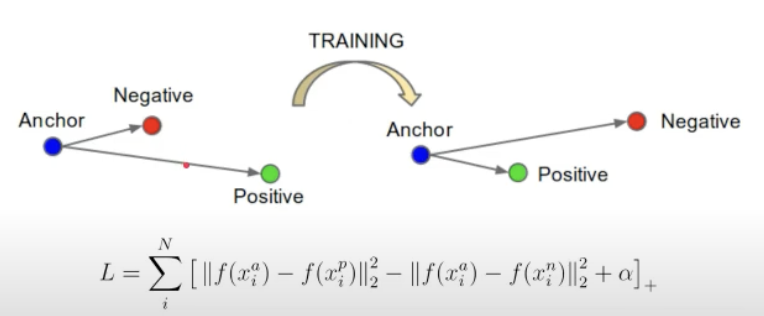
Anchor와 positive의 거리가 negative와의 거리보다 가까워지도록 만들어야합니다.
수식에서 +의 의미는 양수일 때만 값을 가지고 음수일 때는 0으로 준다는 뜻입니다.
데이터는 어떻게 정할까요?
Metric learning의 장점이 label이 필요 없는 것입니다.
따라서 데이터를 수집할 때 positive는 사람들이 선택한 것, negative는 무작위로 형성합니다.
그러나 negative를 무작위로 고를 경우 모델이 문제를 구분하기 너무 쉬어져 문제가 발생합니다.
그 해결방법으로 online negative mining이 있습니다.

첫 번째 줄에 대해 학습을 진행할 때, 초록색으로 표시된 Anchor와 negative관계를 가지는 것을 배치단(밑에 있는 데이터)에서 무작위로 뽑아 전부 비교를 해봅니다.
이것을 하기 위해서는 배치의 크기가 커야 하는데 GPU에 전부 실지 못해 학습의 어려움을 가져올 수 있습니다.
Contrastive Learning
Contrastive Learning은 input에 대하여 distance가 0(similar) 또는 1(dissimilar)로 계산하며 학습하는 과정입니다.
similar한 것과 dissimilar한 것 각각 loss function을 다르게 사용하여 학습합니다.
$$ L(W, X, \vec{X}_1, \vec{X}_2)^i = (1 - Y)\,L_S(D^W_i) + Y\,L_D(D^W_i) $$
위 수식에서 첫 번째 항은 similar할 때 사용하고 두 번째 항은 dissimilar할 때 사용합니다.
이 Contrastive learning를 통해 softmax를 재해석해 볼 수 있습니다.
softmax는 positive 값을 분자에 모든 negative 값을 분모에 둬 계산하는 과정으로, positive는 더 크게 negative는 더 작게 만드는 과정으로 생각할 수 있습니다.
class의 개수가 많을 경우 softmax의 분모 계산 때 많은 시간이 소요됩니다.
몇 개의 값을 제외한 대부분의 class값이 0에 가까울 정도로 몹시 작으므로 이런 연산은 소모적일 경우가 많습니다.
이를 해결하기 위한 방법으로 Negative sampling이 있습니다.
Negative sampling은 negative 한 item 몇 개만 추출하여 분모를 계산할 때 사용합니다.
수학적으로 봤을 때 이상할 순 있으나 실험적으로 봤을 때 전부 계산하는 것과 비슷한 결과를 가집니다.
이와 비슷한 개념으로 Noise Contrastive Estimator가 있습니다.
real pair를 가진 분포 \(p_m\)과 fake pair를 가진 분포 \(p_n\)을 만들어 binary classification을 합니다.
따라서 logistic regression 문제로 변형됩니다.
Noise Contrastive Estimator의 loss function을 살펴보면 다음과 같습니다.
$$ \sum_{i=1}^M \ln\bigl[h(\mathbf{x}_i; \theta)\bigr] \;+\; \sum_{j=1}^N \ln\bigl[1 - h(\mathbf{y}_j; \theta)\bigr] $$
loss function의 첫 번째 항은 M개만큼의 real pair이고 두 번째 항은 N개만큼의 fake pair입니다.
따라서 maximize 하는 방향으로 학습하면 됩니다. 이는 결국 \(p_m\)을 높이고, \(p_n\)을 낮추는 과정과 동일합니다.
'Machine learning & Deep learning' 카테고리의 다른 글
| [Deep learning] Multi-Modal learning Part1 (0) | 2025.02.27 |
|---|---|
| [Machine learning]Energy-based Models(part1) (0) | 2025.02.27 |
| [Deep learning] BERT 개념과 Minimalist Version of BERT 구현해보기 (0) | 2025.02.20 |
| [Deep learning] Transformer 자세히 공부한 것.. (0) | 2025.02.18 |
| [Deep learning] Transformer에 대한 기본 아이디어 (0) | 2025.02.17 |