Protein structure 예측과 관련된 연구에 관심이 생겨 structured prediction에 대해 공부해 봐야겠다고 생각했다.
2016년 ICML에 publish 된 논문이다.
Paper를 review하기 보단 강의 slide가 있어 이 내용을 순차적으로 공부해보려 한다.
Background
한 입력에 대해 복수의 label을 예측하는 문제인 Multi-label Classification 시 label 간의 관계를 어떻게 잘 파악할지에서 시작한다.

다음과 같이 다양하게 label을 예측할 수 있는 것이다.
multi-label을 예측하는 방법 중 가장 흔히 쓰이고 편한 것이 Independent Prediction이다.
이 prediction은 각 label을 독립적으로 예측하고 라벨 간의 상호작용을 전혀 반영하지 못한다.

Joint Prediction은 label 간의 상호작용까지도 모델링하기 위해 Energy-based model을 이용한다.
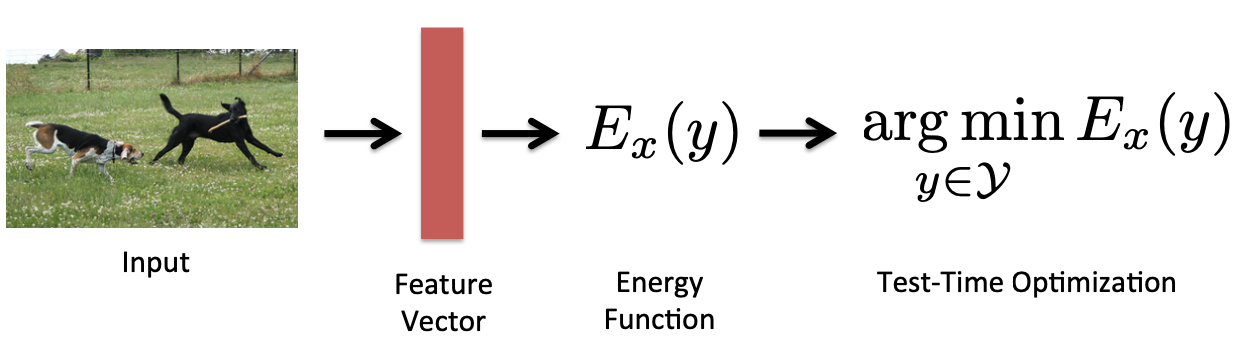
input x에 대해 여러 feature가 생기고 x와 y pair를 energy model에 입력으로 하여 에너지가 가장 낮은 pair를 찾는다.

joint prediction을 할 수 있는 method는 다음과 같은데 이 내용들은 다음에 공부해 보록하자.
이런 joint prediction은 feed forward 방식이 아닌 Test-time optimization으로 학습한다.
둘의 차이점은
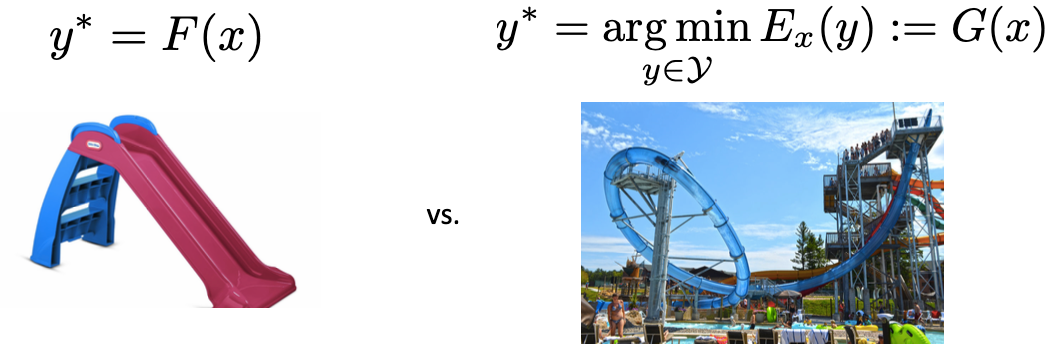
feed forward 방식은 예측값을 한 번에 출력하는 대신 test-time optimization은 t시점마다 y의 값을 확인하고 조정하면서 학습을 한다.
feed forward는 y를 예측하는 것이라면 test-time optimization은 enery score에 따라 y를 조금씩 수정하는 것이다.
특히 이 구조는 domain knowledge를 반영할 수 있으며 미분이 가능하여 backpropagation이 가능하다.
항상 모델을 설계할 때, 계산량과 표현력은 trade-off 관계에 있는데 SPEN은 이 사이에서 균형점을 찾으려는 시도다.
join prediction 기반 학습은
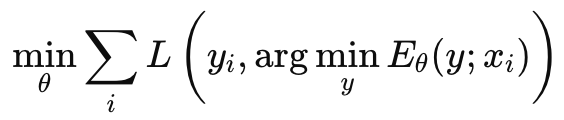
argmin연산을 통해 이뤄지는데 이는 계산이 매우 어렵다.
따라서 근사하여 계산을 해야 하는데

SPEN에서는 projected gradient descent, entropic mirror descent 등을 사용해서 계산을 한다.
Structured Prediction's goal은
- 입력 \(x\)와 출력\(y\) 사이의 중요한 상호작용을 모델링하는 것이다.
- \(y\)는 단순한 형태가 아니라 복잡한 구조일 수 있다. 따라서 가능한 \(y\)들을 combinational 하게 탐색해야 한다.
이지만 어려운 task일 뿐만 아니라 modeling 하는 것도 computationally expensive 하다.
Motivation for SPEN
neural network를 이용하여 Structure prediction을 해보자.
neural network는 입력 \(x\)에 대해 feature representation을 몹시 잘한다.
이러한 특정을 structured prediction문제에 적용하는 것이다.
즉, 출력 \(y\)도 서로의 관계 및 구조가 있으므로 이를 neural network로 학습할 수 있지 않을까?라는 물음에서 시작한다.
SPEN의 구조와 학습하는 과정을 봐보자.
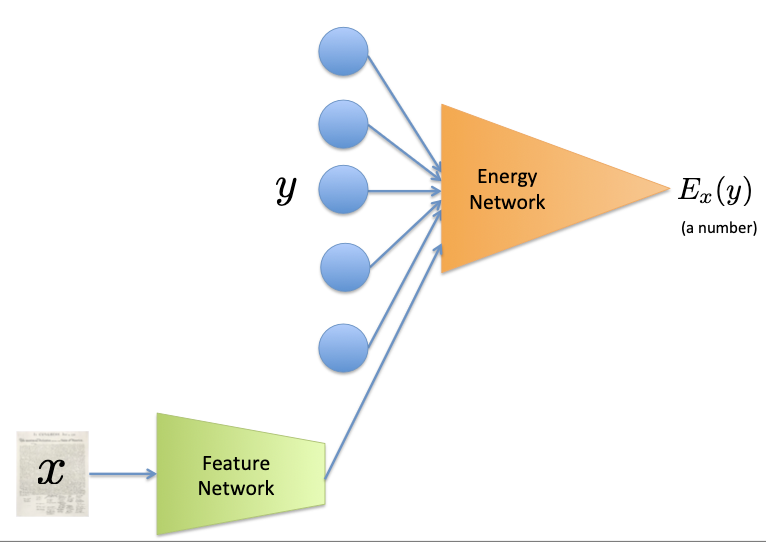
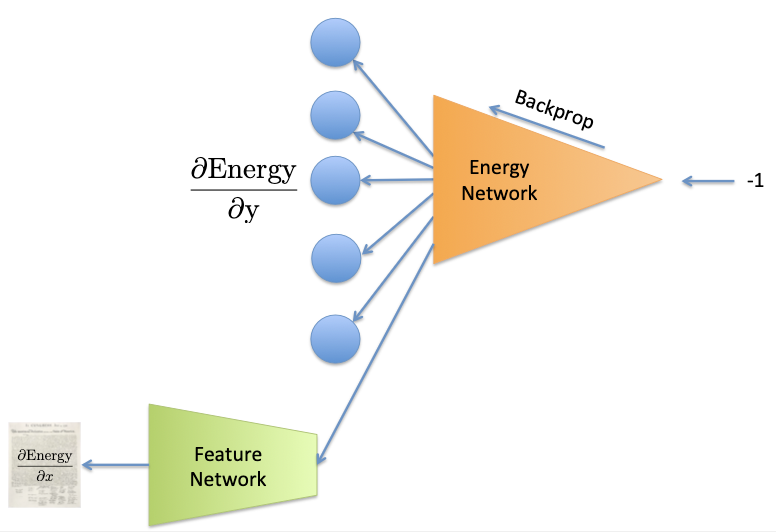
SPEN의 구조는 크게 Feature Network와 Energy Network로 구성된다.
입력 \(x\)에 대해 feature vector로 나타내서 예측할 출력 \(y\)와 함께 Energy Network에 입력으로 사용한다.
이때, 각 pair에 대해 Scalar Energy score를 출력하고 그 값을 기준으로 backpropagation을 하여 학습한다.
SPEN의 핵심은 test-time에 gradient descent로 \(y\)를 최적화하는 것이기 때문에 \(y\)에 대해 미분가능해야 한다.

이와 같이 매 time마다 \(y\)를 update 해주고 예측(inference)할 때도 backprop을 사용한다는 점에서 독특하다.
또한 여기서 중요한 개념인 Convex Relation을 알아야 한다.
Convex Relation이란 이산공간에서의 최적화를 연속공간으로 바꾸어 tractable 하게 만드는 것이다.
예를 들어 binary classification 문제에선 라벨 \(y_i\)는 0 또는 1만 가진다.
이 경우 가능한 조합의 수는 \(2^L\)인데, 이는 최적화하기 힘들다.
Convex Relation이란 라벨\(y_i\)가 0 또는 1만 가진던 것을 0과 1 사이의 실수 값을 가질 수 있도록 하는 것이다.
따라서 각 step마다 \(y\)를 업데이트시키고 [0,1]의 범위를 넘지 않게 projection을 수행한다.
최종값은 rounding 해서 0 또는 1로 이산적으로 변환가능하다.

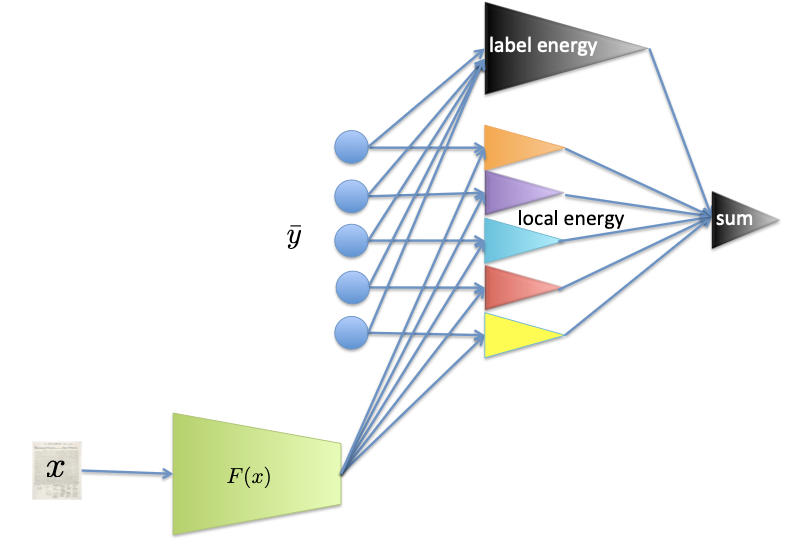
- Feature Network: Multi-layer perceptron
- Energy Network: Local Energy와 Label Energy로 구성
Local Energy
각 라벨 \(y_i\)에 대해 독립적인 scoring을 수행하는 것이다.
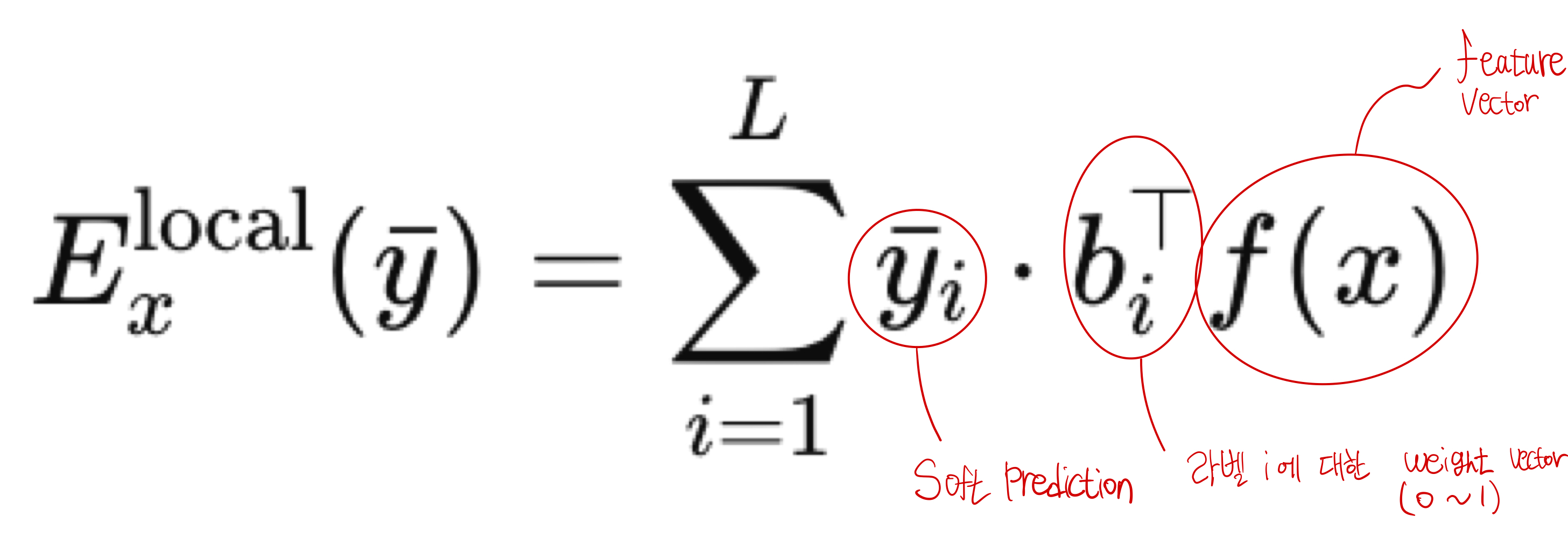
각 라벨 별로 \(x\)와의 score를 계산하고 총합을 구해 energy score를 출력한다.
Label Energy
라벨 간의 구조적인 상호작용을 모델링한다.
즉, 라벨끼리 어떤 관계를 맺고 있는가?를 학습한다.
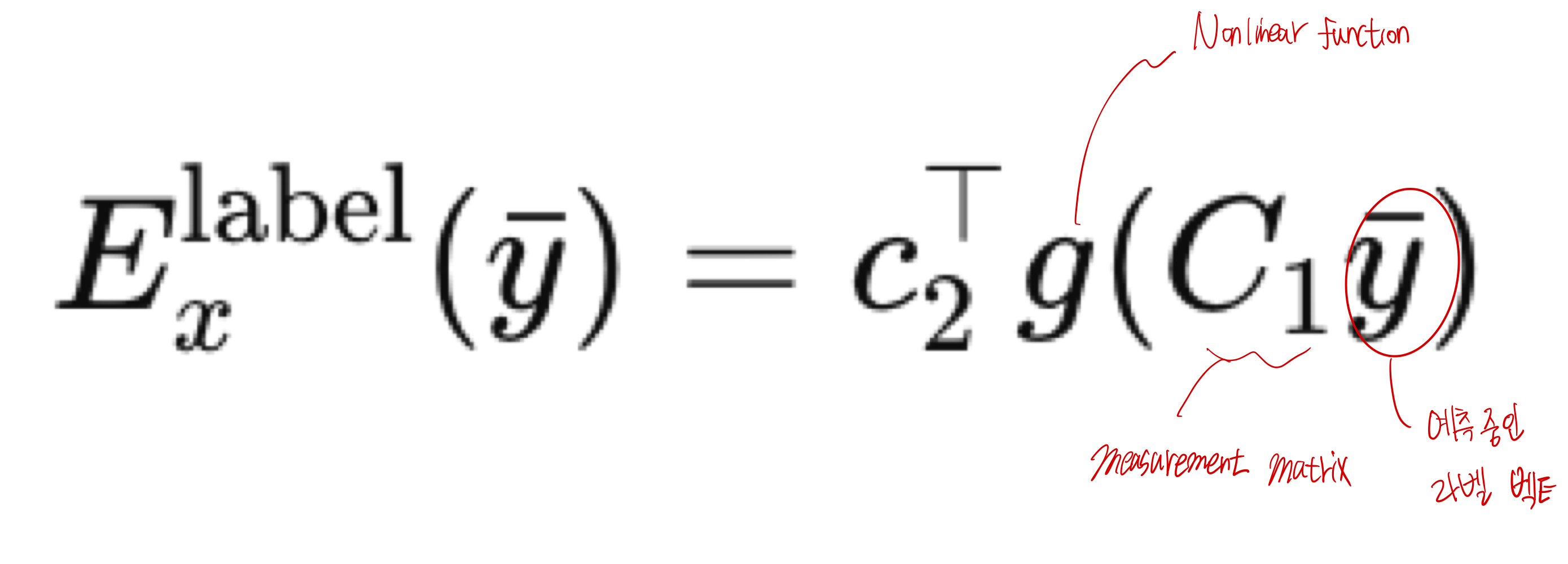
Measurement Matrix는 예를 들어 100개의 라벨이 있다고 치면, 차원이 100으로 \(y\)들 간 다양한 조합으로 projection 하여 서로의 관계를 학습할 수 있도록 한다.

학습은 다음과 같이 한다.
여기서는 MSE loss를 사용할 수없기 때문에 Structured SVM loss 기반의 loss를 사용하는데..
MSE loss는 단순히 정답만 맞추는 것, 틀린 예측들이 얼마나 헷갈리는지는 신경 쓰지 않는다.
따라서, 예측 공간이 거대하고 복잡하면 가장 헷갈리는 오답을 잡아내야 성능이 올라간다.
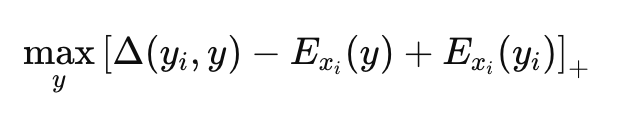
즉 이 수식은 정답 \(y_i\) 보다 틀린 예측 \(y\)가 더 낮은 energy를 가지면 안 된다.
모델이 헷갈려하는 \(y\)를 찾아서 최적화하는 것이다.
\(y\)를 헷갈려한다는 것은 모델이 착각해서 낮은 energy를 주는 거고 이는 SVM loss값을 키우게 된다.
그런 \(y\)를 찾아서 최적화하는 것이다.
SPEN의 loss를 다시 살펴보면
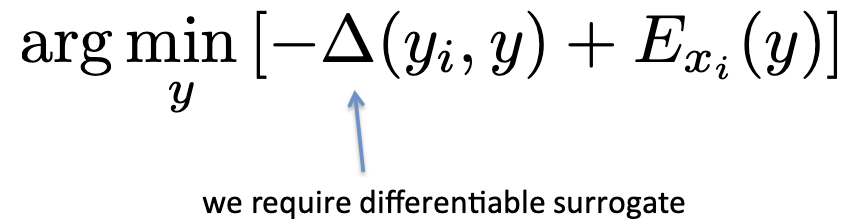
다음과 같이 표현할 수 있다.
위 내용과 일맥상통하다.
모델이 정답을 헷갈려할수록 \(\left [ \Delta(y_i, \bar {y}) \right]\)은 커지고 \(E_{x_i}(y)\)는 작아진다.
따라서 음수값 이므로 더 작아질 텐데, 그때의 \(y\)를 찾는 것이다.