뉴립스 2024 workshop 중 관심 있던 Paper에 대해 리뷰해보려고 하는데요.
정말 다양한 주제가 있지만, 그중에서도 AI가 수학적인 추론 부분에서 얼마나 잘하는지에 대해 궁금증을 가져 이 내용에 대해 알아보려고 합니다.
제가 MATH-AI에서 리뷰할 논문은 How Far Can Transformers Reason? The Globality Barrier and Inductive Scratchpad입니다.
다음과 같은 순서로 리뷰할 예정입니다.
Agenda
Summary
Problem
- Syllogisms composition
- Hardness of long compositions
- Hardness of global reasoning
Solution
- Definition: Globality degree
- Scratchpad
Future Work
Summary
논문에서는 크게 How can we formalize the ‘global reasoning barrier’ in general term? 와 Can we break the ‘global reasoning barrier’ with scratchpad methodologies?이라는 두 물음에 대해 답하는 방식으로 진행합니다.
Q1: global reasoning barrier 정도를 어떻게 평가, 공식화할 것인가?
A: Globality degree: Transformer가 정답을 예측하기 위해 필요한 최소한의 토큰 개수

degree가 높을수록 전역성이 높아 학습이 어려움!
Q2: global reasoning barrier를 scratchpad을 이용하여 해결할 수 있을까?
A:
| Agnostic | Educated | Inductive | |
| 특징 | 중간 과정 기록 없이 추가 메모리만 제공 | 문제를 하위 문제(Subtasks)로 나누어 학습 | 귀납적으로(step-by-step) 학습 |
| 장/단점 | 별 효과 없음 | 학습 가능성(Learnability) 증가& OOD 일반화 성능 부족 | OOD 일반화 성능 향상 |
Problem
Syllogisms composition

추론 중 가장 기본적인 삼단논법에 대한 예시 인데요.
transformer는 길이가 긴 삼단논법에 대해 잘 판단을 못하는 것으로 알려져 있습니다.
삼단논법으로 graph-based task를 직접 해결하는 것이 목표가 아니라, 기존의 정보를 ‘어떻게 조합' 할 것 인지와 ‘어디까지’ 조합할 수 있는지에 초점을 맞추고 있네요.
Cycle Task
삼단 논법과 비슷하게 transformer가 잘못할 것 같은 task를 저자들이 Cycle Task라고 정의했는데요.

Cycle Task는 이진분류문제로 쉽게 설명하면 임의의 두 node를 선택했을 때, 그 두 node가 한 cycle에 있는지 없는지 판단하는 문제입니다. 서로의 연결을 계속 파악해야 하기에 global reasoning이 필요한 task입니다.

표에서 보는 것처럼 node의 개수가 6만 넘기려 해도 지수적으로 증가하면서 학습이 어려운 것을 볼 수 있습니다. 모델의 파라미터 개수를 늘리더라도 비슷하게 지수적으로 증가하여 학습이 어려운 것을 볼 수 있네요.
이러한 문제를 해결하기 위해 Globality degree & Scratchpad! 를 정의합니다.
Solution
Globality degree
쉽게 설명하면 모델이 타깃 Y와 비트 수 n에 비례하는 정도로 mutual information을 형성하기 위해 주목해야 하는 최소한의 입력 토큰 수라고 할 수 있어요.


Globality degree에 대한 특징으로 저자들은 4가지로 정리했습니다.
- Explicit measure: 최소한의 토큰수를 계산하는 방식으로 복잡한 이론적 전개 없이도 간단하게 계산하여 정량적으로 평가 가능
- Applicable to Any Data Distribution: 데이터가 ‘어떻게 생겼는지'가 아니라 '얼마나 많은 정보가 필요한지'에 집중하기 때문에 데이터의 구조적 특성에 의존하지 않음
- Not Limited to i.i.d. Inputs
- Relevant to Current Models like Transformers: 패턴인식에 강력한 성능을 보이는 Transformer의 global reasoning에 대한 한계를 명확히 파악할 수 있음
Scratchpad
Scratchpad는 모델이 학습 과정에서 중간 계산 결과나 임시정보를 저장하는 보조 메모리 공간으로 global reasoning이 필요한 문제를 더 효율적으로 처리할 수 있어요. 3가지 종류의 Scratchpad에 대해 설명하는데 장단점과 단점을 어떤 식으로 극복했는지 위주로 보면 좋을 것 같아요.
Agnostic Scratchpad
첫 번째로 소개되는 내용은 Agnostic Scratchpad입니다.입니다.
Agnostic Scratchpad은 직접적인 지시 없이 추가적인 메모리나 계산만을 제공합니다.
주요 특징은 다음과 같아요.
- globality degree가 상수일 경우, weak learning이 가능함
- globality degree가 상수가 아닌 경우, 단순한 메모리 확장으로 학습이 불가능
따라서, weak learning을 하기 위해 Educated Guess based on Target Knowledge이 필요하고 그러한 점을 보완한 것이 Educated Scratchpad입니다.
Educated Scratchpad
Educated Scratchpad는 Agnostic Scratchpad와 다르게 문제를 subtasks로 나누고, 이를 해결할 수 있도록 구체적인 전략을 제시합니다.
Educated Scratchpad를 이용할 경우 transformer가 잘하지 못하는 parities판단과Cycle task에 대해 성능이 올라가는데요.
parities판단은 비트 시퀀스의 1의 개수가 홀수인지 짝수인지를 판단하는 문제로 XOR연산을 통해 결정합니다.
parities 학습의 경우 다음과 같이 Cumulative Product로 지시를 내려 globality degree가 2로 감소시켜 학습을 진행합니다.

Cycle task 학습의 경우 DFS 알고리즘을 적용하여 globality degree를 3으로 낮춥니다.
- 실험: a와 t가 cycle을 형성하는지? a부터 탐색시작
- DFS: 한 노드에서 시작하여 가능한 깊이까지 탐색한 후, 더 이상 갈 곳이 없으면 다시 돌아오는 방식으로 작동


But, it can be sensitive to the number of reasoning steps, translating into poor out-of-distribution(ood) generalization
즉 처음 본 새로운 데이터에 대해서는 판단을 잘하지 못하는데요. 그 이유는 정해진 노드의 길에 대해서만 학습했기 때문입니다. 과적합이 일어난 거죠..

여기서 DFS scratchpad --OOD을 보면 성능이 매우 낮은 것을 알 수 있습니다.
이런 문제를 극복하기 위해 Inductive scratchpad을 정의합니다.
Inductive scratchpad
Inductive scratchpad는 바로 이전 단계의 상태만을 가지고 학습하기 때문에 길이에 대해 의존적이지 않습니다. 이런 특성으로 OOD에 대해서도 일반화가 가능합니다.


<start> 토큰, <eos> 토큰, 상태를 나타내는 # 으로 inductive scratchpad를 표현할 수 있습니다.
Inductive scratchpad을 이용하면 parities판단과 Addition task에 대해서 일반화 성능을 보이는데요.
- generalization for parity
비트 공간에 random space를 삽입하여 특정패턴에 의존하지 않고 독립적으로 처리하도록 합니다. 30 bits로 학습시킨 Transformer가 50~55비트 샘플에 대해서도 일반화 성능을 유지할 수 있어요.

- Length generalization for addition tasks
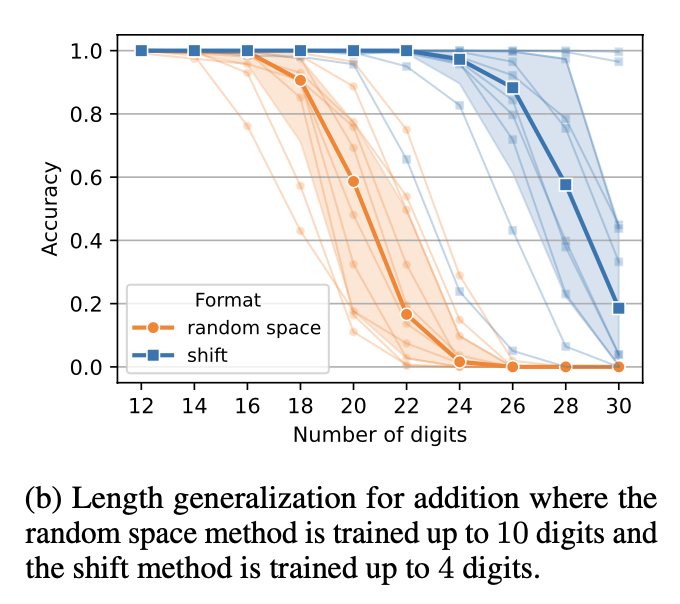
| Random Space Method | Shift Method | |
| 삽입하는 요소 | spaces | random tokens |
| 입력형식의 자연스움 | 자연스러움: 공백은 일반적인 텍스트 형식과 유사 | 비자연적: 무작위 토큰은 입력 형식을 복잡하게 만듦 |
| 자리수 처리 방식 | 공백을 통해 자리수 경계를 명확히 구분 | 토큰을 통해 자리수를 이동시켜 계산 |
| 일반화 범위 | 10자리 → 18자리 | 4자리 → 26자리 |
Future work
- Global leap
현재는 weak learning환경에만 초점이 맞춰져 있음 따라서 Global leap을 통해 더 높은 globality를 요구하는 문제를 해결해야 할 필요가 있어요.
- Inductive Scratchpad의 Inductive reasoning이 새로운 task에도 적용될 수 있는지?
parities, addition문제에 대해서는 전이가능하다고 보고 추후 다양한 유형의 문제에 적용가능한지 확인 필요합니다.
이상으로 transformer가 수학 문제를 풀 때 global reasoning을 잘하나? 잘하기 위해서는 어떻게 해야 하며 어떻게 평가를 해야 하는지에 대해 알아봤습니다.
https://nips.cc/virtual/2024/workshop/84719
MATH-AI: The 4th Workshop on Mathematical Reasoning and AI
Mathematical reasoning is a fundamental aspect of human cognition that has been studied by scholars ranging from philosophers to cognitive scientists and neuroscientists. Mathematical reasoning involves analyzing complex information, identifying patterns a
nips.cc
을 방문하시면 저자의 talk을 들으실 수 있어요.
https://github.com/aryol/inductive-scratchpad
GitHub - aryol/inductive-scratchpad: Implementation for our paper "How Far Can Transformers Reason? The Locality Barrier and Ind
Implementation for our paper "How Far Can Transformers Reason? The Locality Barrier and Inductive Scratchpad" - aryol/inductive-scratchpad
github.com
저자들이 git에도 배포해 놨으니 참고하시면 좋을 것 같네요~~