오늘은 Overfitting을 해결하기 위한 방법인 Ridge Regression을 알아보겠습니다.
Ridge Regression의 수식에 대해 자세하게 분석해 보면서 어떻게 Overfitting을 해결하는지 알아보겠습니다.
일반적인 선형 회귀는 최소제곱법을 사용하여 아래의 cost function을 최소화합니다.
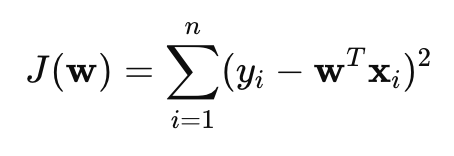

학습 중 feature들 간의 상관관계가 너무 높으면 계수 w가 너무 커져 Overfitting이 될 수 있습니다.

이제 Cost function에 Regularization Term을 추가하여 학습하는 과정을 설명드릴게요. 학습 시 Cost function을 최소화하는 w을 찾는 방향으로 학습이 진행됩니다.
이때, λ의 값이 있을 경우 전체 Cost function을 최소화시켜야 되는데 Regularization Term이 있으므로 이것을 최소화하는 방향으로 학습을 해야 돼요.
그니깐 값이 없어야 되는 데 있을 거라면 최소로 있으라는 느낌입니다.
이런 방향으로 학습이 이뤄지다 보니 w를 없애는(최소화) 방향으로 학습을 진행합니다.
λ가 커질수록, w를 더 크게 줄여 과적합을 방지합니다.
Cost function을 w에 대해 미분을 해서 0이 되게 하는 w을 찾아서 w가 어떻게 되는지 살펴볼까요?
비용 함수 \( J(\mathbf{w}) \)를 \( \mathbf{w} \)에 대해 미분하면:
\[ -2\mathbf{X}^T \mathbf{y} + 2\mathbf{X}^T \mathbf{Xw} + 2\lambda \mathbf{w} = 0 \]
양변을 2로 나누면:
\[ \mathbf{X}^T \mathbf{Xw} + \lambda \mathbf{w} = \mathbf{X}^T \mathbf{y} \]
최종적으로 Ridge Regression의 해:
\[ \mathbf{w} = (\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^T \mathbf{y} \]

이 값을 살펴보면 \( (X^{T}X+\lambda I) \) 항이 역수로 곱해지기 때문에 \(\lambda\) 가 커질수록 \( (X^{T}X+\lambda I) \) 항이 커지므로 \( W \)는 작아지는 것을 알 수 있어요!!
Ridge Regression와 같이 비교할 수 있는 개념으로 Lasso Regression은 정규화도 있습니다.
간단하게 짚고 넘어가면 Lasso Regression은 타깃과 예측값 차의 제곱을 이용하는 Ridge Regression와 다르게 절댓값을 이용해요.
따라서, Lasso Regression은 W를 완전히 0으로 보내버려서 Overfitting을 해결해요.
오늘은 오버피팅 문제를 해결할 수 있는 Ridge Regression에 대해 수식적으로 알아보았습니다.
'Machine learning & Deep learning' 카테고리의 다른 글
| [Deep learning] Transformer 자세히 공부한 것.. (0) | 2025.02.18 |
|---|---|
| [Deep learning] Transformer에 대한 기본 아이디어 (0) | 2025.02.17 |
| [Deep learning] Attention Mechanism에 대하여 (0) | 2025.02.16 |
| [Deep learning] LSTM과 GRU를 Vector combination 관점에서 살펴보기 (0) | 2025.02.16 |
| [Machine learning] Dropout 내가 궁금했던 모든 것 정리 (0) | 2025.02.15 |