오늘 공부할 내용은 저번에 공부한 Decision Tree의 성능을 향상하기 위한 방법이다.
[Machine learning] Tree based Methods: Decision Tree로 Regression과 Classification하기
Tree-based Methods분류와 회귀 작업 모두에 사용 가능하며, 입력공간을 재귀적으로 분할하여 단순한 영역으로 나눈다.이 방법은 시각적으로 이해가 쉽고, 해석력 높은 모델을 만들 수 있다. 단, 정
ysk1m.tistory.com
사실 오늘 정리한 내용은 Decision-Tree뿐만 아니라 machine learning의 성능을 향상하기 위한 general 한 method이다.
실제로 연구할 때는(paper를 쓸 때) 자신 연구의 novelty를 강조하기 위해 Bagging, Random Forests, Boosting을 쓰지 않는다.
쓰면 어차피 좋아질 테니깐...
그러나 회사와 같은 산업계에 높은 성능의 모델을 만들려면 무조건 쓰는 게 좋다.
Bagging, Boosting, Random Forest 셋 다 모델의 성능을 좋게 많든다고 했는데 구체적으로 어떤 성능을 어떻게 좋게 만들어 줄까?
먼저 공통적인 효과는 출력의 variance를 낮춰 좀 더 안정적이게 출력을 할 수 있다.
그럼 이제 각 method에 대해 자세히 알아보자.
Bagging method
Bagging은 쉽게 말해 Decision-Tree에 Bootstrap을 적용하는 것이다.
Dataset은 제한적이므로 여러 experiment를 할 수 없는데 이때 사용할 수 있는 것이 Bagging이다.
말한 대로 single training dataset에서 반복적으로 추출하여 여러 개의 데이터셋을 생성한다.
Regression 문제에서는

다음과 같이 표현할 수 있다.
\(B\) 개의 다른 bootstrapped data에 대해 각각 예측해서 평균을 내는 것이다.
Classification 문제에서는
동일하게 각 bootstrapped data에 대해 하나의 qualitive response를 출력하고 majority vote를 이용하여 가장 많이 예측된 Class를 정답으로 한다.
저번 게시글에서 예시로 들었던 Heart data에 대해서 test error를 나타낸 그래프이다.
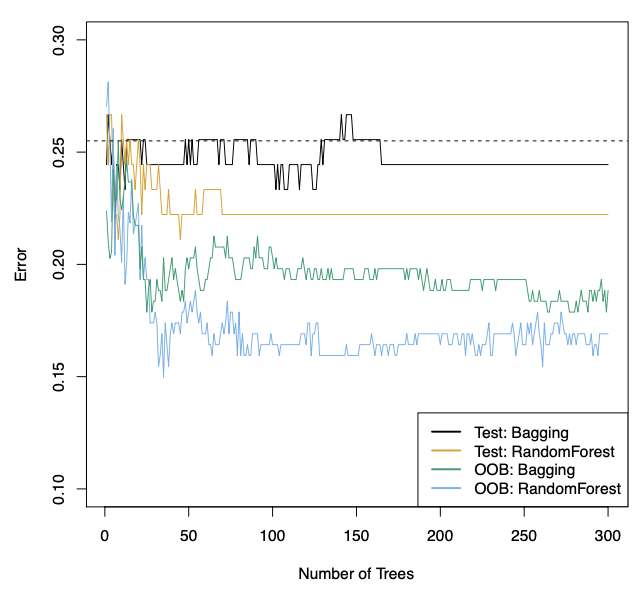
bagging이 Single Decision tree인 검은색 점선보다 월등하게 test error가 낮은 것을 볼 수 있다.
test erro r면 오른쪽(feature가 많아진 경우)으로 갈수록 overfitting으로 인해 error가 올라가야 될 것 같은데 이 그래프는 그렇지 않다.
그 이유는 tree를 많이 늘리는 것은 많은 tree의 결과를 평균화하여 variance를 감소시키기 때문이다.
그래서 그래프를 보면 overfitting이 일어나지 않은 것이다.
즉, bagging에서 tree의 개수를 늘리면 데이터를 많이 학습시키는 것이니깐 overfitting이 일어난다고 생각할 수 있지만 실제로는 그렇지 않다.
OOB는 Out-of_Bag으로 bootstrap에서 사용하지 못한 데이터를 validation set을 이용한 것이다.
그렇다 보니 test set에 대해 원래 방법들보다 성능이 훨씬 좋다.
그러나, tree를 많이 늘려도 특정 개수 이상이 되면 더 이상 성능이 좋아지지 않는다.
그 이유는 중복된 데이터들이 결국 이용될 거고 각 tree끼리 correlation이 생기기 때문이다.
Random Forests
이렇게 tree들끼리 서로 correlation이 있는 것을 decorrelate 하기 위한 방법이 Random Forest이다.
bootstrap data를 이용하는 것까지는 동일하다.
bootstrapped data에서 tree를 만들 때 각 internal node에서 이용하는 feature를 다르게 하는 것이다.
p개의 predictors가 있다면 그중 무작위로 m개의 predictors를 골라 internal node에서 m개의 predictors 중 1개를 기준으로 split 한다.
즉, 이름에서의 random이 predictors를 무작위로 뽑기 때문에 붙은 것이다.
대게 random으로 뽑는 feature \(m\) 개는 \(\sqrt p)\)(p는 전체 feature개수)을 따른다.(그때가 성능이 젤 좋음)

m의 값에 따른 classification error를 나타낸 것이다.
m=p일 때는 bagging과 동일하며 당연히 성능이 젤 안 좋다.(random forest가 bagging을 보완한 거니깐)
\(m=\sqrt p\) 일 때 가장 성능이 좋은 것을 알 수 있다.
Boosting
Boosting에서는 bootstraped data를 사용하지 않는다.
single dataset에 대해 sequential 하게 학습하는 것을 말한다.
전에 있던 결과를 받아 순차적으로 모델을 개선해 나가는 것이다.
각 단계에서 새로운 tree를 추가하여 이전 트리가 예측하지 못한 부분을 집중적으로 개선한다.
예측하지 못한 부분을 집중하는 boosting은 residual를 예측하고 그것을 줄이는 것에 초점을 맞춰 학습한다.
boosting 알고리즘에 대해 살펴보면
input으로 single dataset \(\{x_i, y_i\}_{i=1}^n\), \(B\) 개의 tree가 들어온다.
처음에는 모든 \(x_i\)에 대한 예측값을 0으로 세팅하고 오차를 \(y_i\)라 정한다.
아직 아무런 모델이 없기 때문에, 모델이 전혀 예측을 하지 않은 상태이다.
각 단계를 반복하면서(1부터 B번까지)
현재 단계에서 남아있는 잔차를 예측하도록 d번의 split을 가지는 subtree를 만든다.
그 tree를 예측함수에 바로 더하지 않고 shrinkage factor \(\lambda\)를 곱해 더한다.
shrinkage fator를 통해 너무 급격히 변하지 않도록 해서 overfitting을 방지한다.
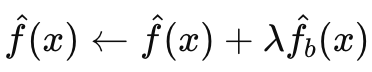

새로운 subtree를 추가해 예측값이 개선되었기 때문에, residual를 새롭게 update 한다.
즉 앞으로 학습할 tree는 현재의 잔차에서 아직 예측되지 않은 부분만을 중점적으로 학습한다.
이런 B개의 d번의 split을 한 subtree들이 모여 최종 boosting모델을 다음과 같이 만든다.
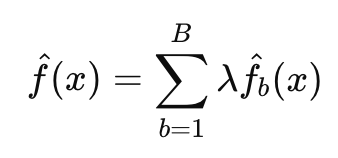
이 방법은 하나의 큰 tree로 data를 fitting 하는 것이 아니라 천천히 오류를 줄여가며 배우는 방법이다.
classification에 대해서도 비슷하게 하는데 더 복잡해서 간단하게만 알아보면
classification문제에 맞는 손실함수를 정의하고, 각 단계에서 그 손실의 잔차를 예측하도록 하는 것이다.

보는 것처럼 random forest보다 성능이 좋으며 split 개수가 d=1인 subtree로 구성된 boosting방법이 성능이 더 우수한 것을 알 수 있다.
boosting의 성능을 향상하기 위한 parameters로 tree의 개수(B), shrinkage factor(\(\lambda\)), 각각의 tree들이 얼마나 split 하는지(d) 이 있다.
각 parameter가 변함에 따라 모델의 성격이 어떻게 달라지는지 알아보겠다.
- Number of trees(B) : tree의 개수가 많아질수록 bagging과 random forest와는 다르게 overfitting이 일어날 수 있다. single dataset에 대해 residual를 낮추는 방향으로 sequential하게 학습되기 때문에 tree의 개수가 많다면 overfitting이 일어날 수 있다.
- Shrinkage factor(\(\lambda\)): shrinkage factor는 작을 수록 천천히 학습 하기 때문에 tree의 개수가 많아야한다. 또한 천천히 학습하기 때문에 local solution에 빠질 위험이 적고 noisy를 한번에 과하게 학습하지 않아 overfitting의 가능성이 줄어든다.
- Number of splits(d): boosted ensemble의 복잡도를 조절하는 것으로 subtree의 깊이를 나타낸다. d가 1일때 잘 작동하는 것으로 알려져 있고 d가 클수록 interaction을 더 잘 반영한다.


첫 번째 그래프를 보면 GBM이 확실히 부드럽게 학습되는 것을 확인 할 수있다.
두 번째 그래프는 3개의 ensembles 기법중에서 Gradient Boosting이 성능이 가장 좋다.

bagged/ RF regression tree의 경우 한눈에 보기 힘드므로 다음과 같이 RSS 기준으로 가장 많이 기여한 predictors를 표시할 수있다.
classification의 경우 Gini index를 사용하여 그 성능을 확인할 수 있다.
Summary
decision tree와 같은 tree based method를 사용하는 이유는 simple하고 interpretable하기 때문이다.
그러나 prediction accuracy 측면에서는 다른 모델보다 성능이 좋지않다.
이러한 한계를 ensembles를 통해 해결하였고 supervised learning에서는 sota 모델이다.
그러나 여러 tree를 합친다는 점에서 interpretability가 떨어졌다.