이번 글은 이준석 교수님의 Generative Models 2 강의를 참고하여 공부한 내용입니다.
Generative Adversarial Networks
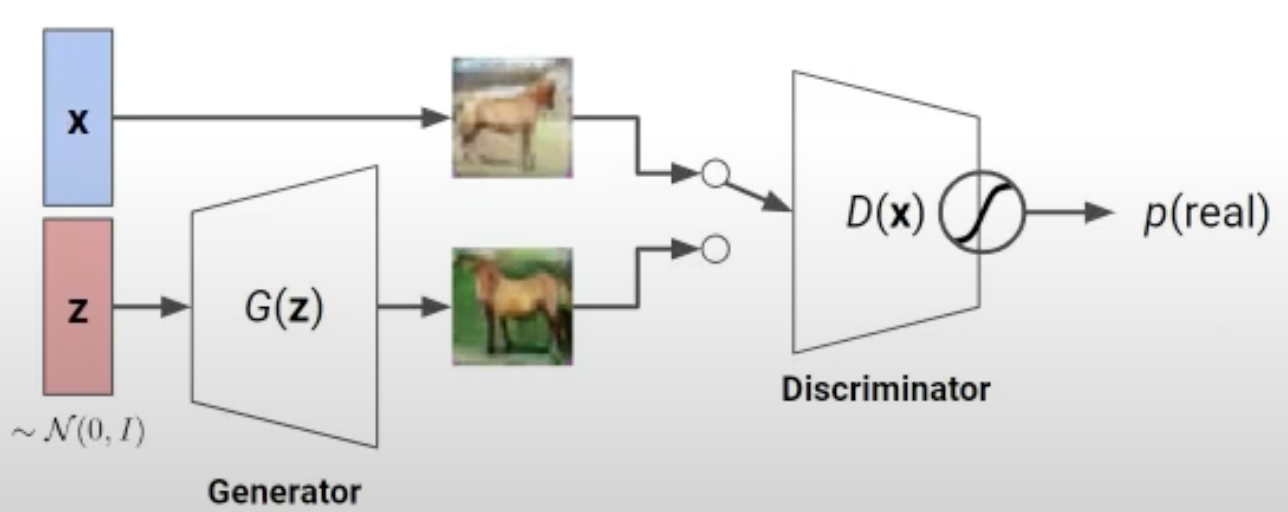
GAN은 다음과 같이 데이터를 생성하는 Generator와 생성한 것과 진짜 데이터를 구분하는 Discriminator로 구성돼 있습니다.
서로 경쟁하며 학습을 하는데요.
Generator는 Discriminator가 잘 구분 못하게 해야 하고 Discriminator는 Generator가 생성한 데이터인지 진짜 데이터인지 구분해야 합니다.
Discriminator는 real vs fake binary classification(cross-entropy)을 해야 합니다.
따라서 objective function은 다음과 같습니다. $$
\max_{\theta_d} \Bigl[
\mathbb{E}_{x \sim D}\,\log D_{\theta_d}(x)
\;+\;
\mathbb{E}_{z \sim p(z)}\,\log\bigl(1 - D_{\theta_d}\bigl(G_{\theta_g}(z)\bigr)\bigr)
\Bigr]
$$
첫 번째 항은 real image \(x\)가 들어왔을 때맞춰서 1이 나오게 해야 됩니다.
두 번째 항은 fake image \(z\)가 입력이므로 0이 나와야 하고 max를 구해야 하므로 \(1 - D_{\theta_d}\bigl(G_{\theta_g}(z))\) 형태로 써줍니다.
Generator는 discriminator를 속여야 하므로 fake image(0)가 discriminator로 들어갔을 때 real image(1)로 판단하게 해야 합니다.
따라서 objective function은 다음과 같습니다. $$
\min_{\theta_g} \Bigl[
\mathbb{E}_{z \sim p(z)}\,\log\bigl(1 - D_{\theta_d}\bigl(G_{\theta_g}(z)\bigr)\bigr)
\Bigr]
$$
이 둘을 합치면 $$
\min_{G}\,\max_{D}\; V(D,G)
\;=\;
\mathbb{E}_{x \sim p_{\mathrm{data}}(x)}\bigl[\log D(x)\bigr]
\;+\;
\mathbb{E}_{z \sim p_z(z)}\bigl[\log\bigl(1 - D\bigl(G(z)\bigr)\bigr].
$$
과 같이 됩니다.
이 objective function은 minimax game으로 trainig이 굉장히 어렵습니다.

먼저 학습을 할 때 loss를 계산하면 점점 줄어드는 형태를 가져야 하는데 loss function이 Dicriminator와 Generator로 이뤄져 있기 때문에 언제 학습이 완료됐는지 정확히 알기 어렵습니다.
또한 GAN 모델 학습은 Generator와 Discriminator을 학습시키는 것입니다.
둘 중 Generator학습하는 것이 더 어려워 대부분의 학습은 Generator에서 일어납니다.
하지만 objective function은 Discriminator로 이뤄져 있기에 이점도 모순이 있습니다.
수학적으로 좀 더 자세히 살펴보면 GAN의 Objective를 최소화는 하는 것은 JS-divergence(KL-divergence와 비슷한 개념)을 최소화하는 것과 동일한 개념입니다.
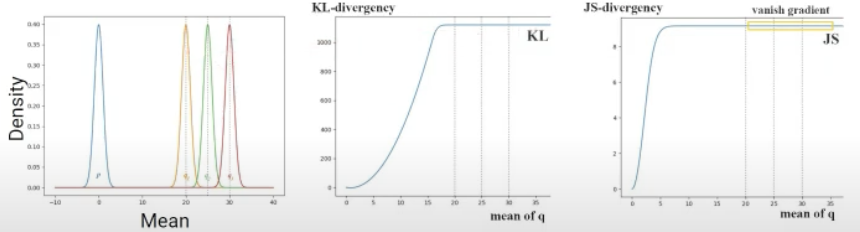

초기에는 \(p_{data}\)와 \(p_{q}\)의 차이가 크므로 gradient가 거의 변하지 않아 학습이 어렵습니다.
위와 같은 Unstable Training 문제뿐만 아니라 GAN의 고질적인 문제에 대해 알아보겠습니다.
그것은 Mode Collapse라는 문제입니다.
Generator가 학습을 쉽게 하려고 whole data space에 대해 generate 하지 않고 특정 sample에 대해서만 generate 하는 것입니다.
이렇게 될 경우 모델의 성능이 몹시 저하됩니다.
이러한 문제를 해결하기 위해 설계한 모델을 소개하겠습니다.
Wasserstein GAN
KL-Divergence를 이용하는 것을 문제로 삼았고 Earth Mover(EM) distance를 제안했습니다.
Objective function의 식은 다음과 같습니다.
$$ \max_{w \in W}\;\Bigl( \mathbb{E}_{x \sim P_r}\bigl[f_w(x)\bigr] \;-\; \mathbb{E}_{z \sim p(z)}\bigl[f_w\bigl(g_\theta(z)\bigr)\bigr] \Bigr). $$
식을 얼핏 보면 초기 GAN의 Objective function과 동일합니다.
차이점은 \(log\)를 제거해 줌으로써 상한, 하한을 없앴습니다.
또한 weight \(w\)을 (-c,c)로 clip 하면 \(f_w()\)가 1-Lipschitz continuous을 만족합니다.
이렇게 함으로써 loss가 떨어지는 모습을 확인하여 언제 학습을 끝낼지 판단할 수 있습니다.

추가적으로 Wasserstein GAN 저자들은 mode collape도 완화했다고 주장합니다.
Pix2pix
Image translation에 사용하는 모델로 semantics는 그대로 유지한 채 한 도메인에서 다른 도메인으로 바꾸는 것입니다.
GAN과 비슷하게 Generator와 Discriminator 각각 학습을 하는 구조입니다.

여기서는 real pair인지 속이고 맞히는 문제라고 설명할 수 있습니다.
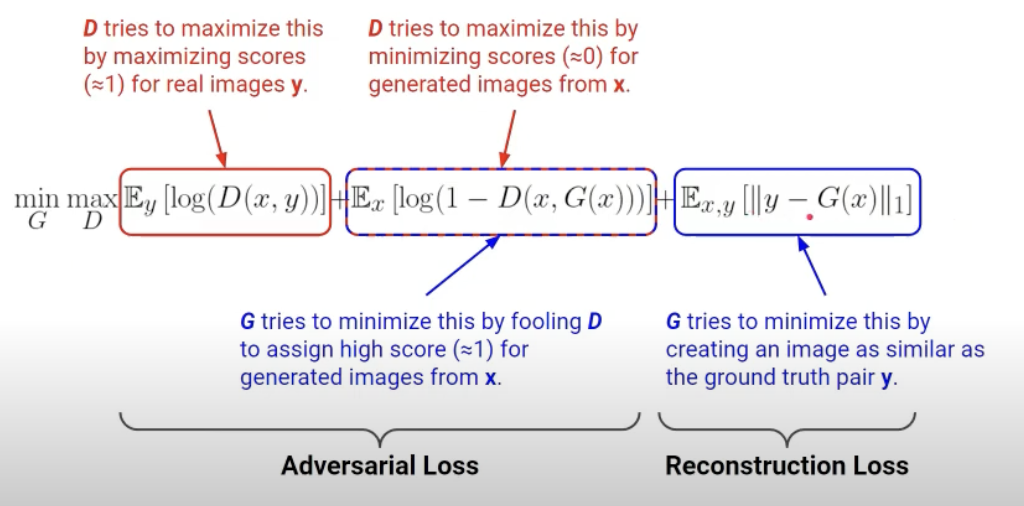
Pix2pix의 objective function으로 첫째항과 두 번째 항은 위에서 본 GAN의 것과 동일합니다.
이 두 개의 항만 있으면 스케치로부터 pair가 아닌 다양한 이미지를 생성하게 됩니다.
모델의 목적은 real pair를 찾는 것이므로 real pair 이미지 \(y\)와 생성한 이미지 \(G(x)\)의 차이(픽셀 단위로 계산)를 줄이는 방향으로 학습합니다.
하지만 Pix2pix를 학습시키기 위해서는 real pair data가 존재해야 하는데 이 pair가 실제 환경에서는 적은 게 한계점입니다.
CycleGAN이 이런 문제를 해결합니다.
CycleGAN
Pix2pix는 한 도메인 \(x\)에서 다른 도메인 \(y\)으로 보내 reconstruction loss를 구합니다.
CycleGAN은 한 도메인 \(x\)에서 다른 도메인 \(y\)으로 보냈다가 다시 도메인 \(x\)로 되돌립니다.

이런 점이 pair가 없이도 학습이 가능한 이유입니다.
예를 들어 Monet 스타일로 스케치를 변형하고 싶다면 정확한 pair는 없지만 Monet의 일반적인 분포가 존재합니다.
GAN loss를 이용하여 이러한 일반적인 분포를 배우고 Cycle-consistency loss를 추가하여 원래 이미지의 정보를 유지한 채로 원하는 스타일로 변환할 수 있습니다.

CycleGAN의 objective function을 살펴보면 다음과 같습니다.
첫 번째 항과 두 번째 항은 위의 GANloss와 동일하므로 설명은 생략하겠습니다.
마지막항은 unpaired 데이터에 대해서 학습할 수 있도록 넣어준 Cycle-Consistency loss입니다.
여기서는 \(x>y>x\)에 대해서만 써 있지만 \(y>x>y\)에 대해서도 동일하게 구해주면 됩니다.

'Diffusion' 카테고리의 다른 글
| [Diffusion] DDPM에 대해 정리한 내용 (0) | 2025.03.28 |
|---|---|
| [Diffusion] VAE (Variational Autoencoder)에 대한 공부 (0) | 2025.03.27 |
| [Diffusion] Generative Models 1 (PixelRNN/CNN, VAE) (1) | 2025.03.02 |