이번 글은 이준석 교수님의 Generative Models 1 강의를 참고하여 공부한 내용입니다.
Generative Modeling
어떤 데이터를 생성하는 probability distribution이 존재한다는 가정하에 이 probability distribution \(P_{model}\)을 예측하는 것입니다.
어떤 new data \(x\)에 대해 우리가 예측한 \(P_{model}\)을 이용하여 새로운 \(P_{model}(x)\)을 생성하는 것입니다.
Generate을 하는 방법은 2가지가 있습니다.
첫 번째는 Explicit density estimation으로 \(P_{model}\)을 수식적으로 예측하여 이용하는 것입니다.
두 번째는 Implicit density estimation으로 \(P_{model}\)을 직접 만들지 않고 생성하는 것입니다.

PixelRNN/CNN
pixel 간의 order가 있다고 생각하고 이 순서대로 다음 pixel을 구현하는 것이 PixelRNN과 PixelCNN의 핵심입니다.
기본적으로 chain rule을 이용하여 image의 likelihood를 계산하는 과정입니다.
$$ p\bigl(X \,\big|\; X_{<i}\bigr) \;=\; p\bigl(X_R \,\big|\; X_{<i}\bigr) \;\times\; p\bigl(X_G \,\big|\; X_{<i},\, X_R\bigr) \;\times\; p\bigl(X_B \,\big|\; X_{<i},\, X_R,\, X_G\bigr). $$
생성하고자 하는 픽셀 전 픽셀(R, G, B)이 어떤 분포를 가지는지를 고려하는 것입니다.
PixelRNN은 RNN 세팅에서 이를 똑같이 하는 것입니다.

다음과 같이 한눈에 표현할 수 있습니다.
먼저 mask 된 입력을 hiddenstate와 함께 입력으로 주고 다음 hiddenstate는 output으로 다음 pixel의 분포를 내뱉습니다.
이후 정답과 loss를 계산하면서 Backprop연산을 하면 됩니다.
이런 세팅을 기본으로 하여 Row LSTM, Diagonal BiLSTM을 설계할 수 있습니다.
RNN을 대신하여 Convolution layers을 쌓아 만든 PixelCNN모델이 있습니다.
parallel 하게 처리할 수 있어 RNN보다 속도가 빠릅니다.
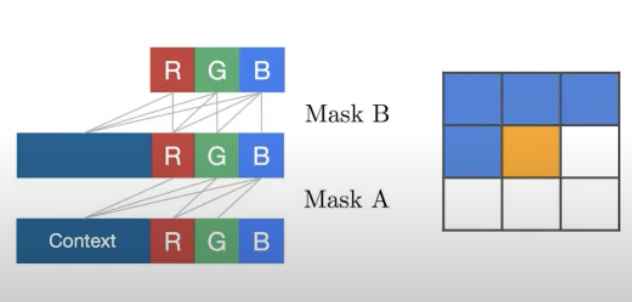
PixelCNN은 예측 전 Pixel에 대한 정보는 mask 하고 이전의 pixel에 대해서만 convolution 연산을 하여 학습시킵니다.
Mask에는 A, B로 두 가지 종류가 있습니다.
Mask A는 첫 번째 층은 실제 pixel을 마주하기 때문에 예측하고자 하는 pixel을 보면 안 됩니다. 따라서 이 부분을 포함하여 mask를 해야 됩니다.
반면에 Mask B는 진짜 pixel을 보는 것이 아니라 convolution filter의 값을 보는 것이기 때문에 그 값을 봐도 됩니다.
Pixel Recursive Super Resolution
Pixel Recursive Super Resolution은 두 가지 데이터를 입력으로 받아 각각 처리해 주고 더한 후 softmax를 계산하여 분포를 결정합니다.
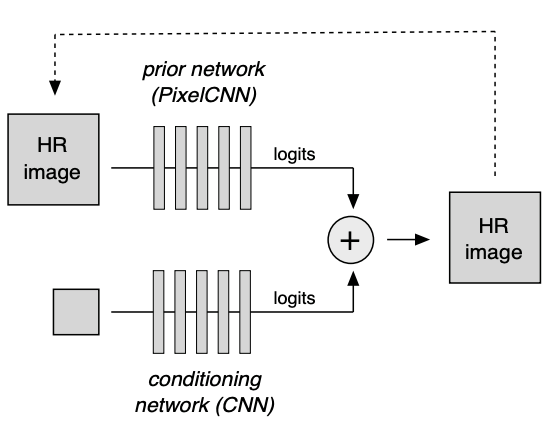
HR image(다음 픽셀 값을 예측해야 하는 이미지)은 PixelCNN을 통과하고 전체 이미지에 대해 참고해 주기 위해 super resolution 전의 저해상도 전체 이미지는 CNN을 통과시킵니다.
이후 이 두 값을 합쳐 확률분포를 예측합니다.
이것을 수식적으로 표현하면 아래와 같습니다.
$$ p(y_i \mid x, y_{<i}) \;=\; \mathrm{softmax}\bigl(A_i(x) + B_i(y_{<i})\bigr) \;=\; \frac{\exp\bigl(A_i(x) + B_i(y_{<i})\bigr)} {\sum_{j}\exp\bigl(A_i(x) + B_i(y_{<i})\bigr)}. $$
여기서 \(x\)는 저해상도 이미지고, \(y_{<i}\)는 기존에 만들어졌던 픽셀입니다.
이제 이것들로부터 \(y_{i}\)를 예측해야 하는 이미지입니다.
PixelCNN을 지난 \(A_i(x)\)와 그냥 CNN을 지난 \(B_i(y_{<i})\)을 softmax연산을 한 것을 알 수 있습니다.
cross-entropy loss를 사용하는데 정답 class에 대해 one-hot encoding을 이용하여 계산해 줍니다.
그러면 다음과 같이 loss function을 정리할 수 있습니다.
$$ \sum_{(x,y^*) \in D} \sum_{i=1}^M \Bigl( 1[y^*_i]^\top \bigl(A_i(x) + B_i(y^*_{<i})\bigr) \;-\; \mathrm{lse}\bigl(A_i(x) + B_i(y^*_{<i})\bigr) \Bigr). $$
또한 특징적인 결과는 같은 input에 대해 다양한 결과가 나올 수 있습니다.
그 이유는 확률 분포의 max값을 sample 하는 것이 아닌 stochastic process로 sampling 하기 때문입니다.
따라서 다음과 같이 비슷하지만 다른 얼굴이 생성됩니다.

지금까지는 확률 분포를 전부 모델링했는데 이제부터는 그 과정이 intracable 해서 approximation이 들어가야 하는 모델에 대해 알아보겠습니다.
Autoencoders
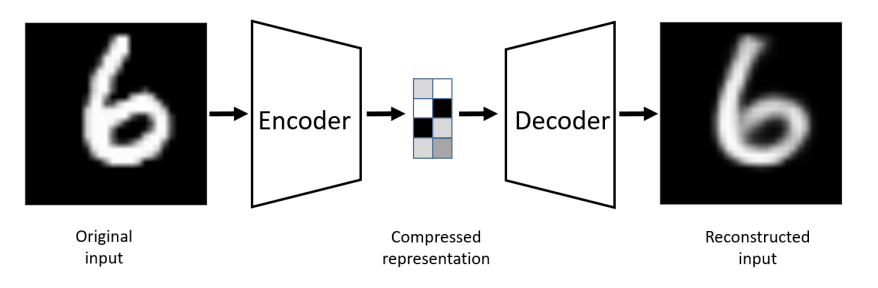
unsupervised approach로 training data를 저차원으로 보내고 다시 고차원으로 복원하며 Encoder를 학습하는 것입니다.
represent learning을 위해 사용되며, 주로 embedding, manifold learning, feature extraction을 수행합니다.
$$ \mathcal {L} \;=\; \sum_{x \in D} \bigl\| x - g\bigl(h(x)\bigr) \bigr\|^2 $$
original input과 reconstructed input의 차이를 비교해 가며 Encoder를 학습합니다.
여기서 Decoder는 사용하지 않는데 Decoder를 이용하여 데이터를 generate 하면 어떨까라는 아이디어가 나옵니다.
맨 처음에 무작위로 Decoder에 입력을 줬으나 잘 생성이 되지 않았습니다.
그러다 Variational Autoencoders라는 개념이 나옵니다.
Variational Autoencoders
Variational Autoencoders에서는 reparameterization trick이라는 개념이 중요합니다.
Compressed representation 영역을 \(z\)라고 하겠습니다.
Autoencdoer에서는 \(z\)를 특정 벡터로 설정하였다면 Variational Autoencoder에서는 \(z\)을 특정확률 분포로 지정합니다.
이 확률 분포로부터 임의로 sampling 하여 decoder에 입력하고 출력값이 원래 값 \(x\)와 유사한지 판단하여 학습을 합니다.
이런 probabilistic models의 stochastic objective에 대해 Gradient based optimization을 할 수 없습니다.
왜냐하면 samplling과정 때문에 backpropagation을 할 수 없기 때문입니다.
따라서 reparameterization trick을 이용하여 이 문제를 해결합니다.
앞서 \(z\)를 특정 확률 분포로 지정한다고 하였는데 가우시안 분포를 따른다고 가정하고 \(\mu\)와 \(\sigma\)를 예측한다고 하겠습니다.
이때 독립적인 분포 \(\epsilon\)을 지정하고 \(z = \mu + \sigma \cdot \epsilon\)와 같이 reparameterization을 합니다.
\(z\)를 \(\mu\)와 \(\sigma\)에 대해 gradient를 구하여 backpropagation을 진행할 수 있습니다.
그럼 이제 loss function에 대해 살펴보겠습니다.
$$ \mathbb{E}_{q_Ø(z \mid x)} \bigl[\log p(x \mid z)\bigr] \;-\; \mathrm{KL}\bigl(q_Ø(z \mid x) \,\|\, p(z)\bigr) \;+\; \mathrm{KL}\bigl(q_Ø(z \mid x) \,\|\, p(z \mid x)\bigr) $$
첫 번째 항은 Reconstruction loss입니다 .
입력 \(x\)와 \(z\)에서 decoder를 지나 reconstruction된 값의 loss를 나타냅니다.
이 loss가 작을수록 원래 입력 데이터를 잘 구성하는 것을 알 수 있습니다.
특히 여기서 입력 데이터 \(x\)를 픽셀값에 대해 one-hot encodding을 하여 classification문제로 전환합니다.
픽셀 값을 확률 분포로 다룰수 있으며, 모델이 보다 자연스럽게 학습할 수 있습니다.
예를 들어 특정 픽셀값을 다음과 같이 표현할 수있습니다.
$$ x_{ij} = 200 \;\;\Longrightarrow\;\; [\,0,\,0,\,\dots,\,0,\;1,\;0,\,\dots,\,0\,] \quad (\text{200번째 요소만 }1). $$
다음과 같이 one-hot encodding한 각각 픽셀에 대해 cross-entropy를 써줍니다.
두번째 항은 Latent space regularization loss입니다.
KL Divergence는 두분포의 거리를 나타내는데 가까울수록(값이 작을 수록) 유사하다고 생각하면됩니다.
따라서 prior distribution인 \(p(z)\)에 model이 학습하고 있는 \(q_Ø(z \mid x)\)이 가까워지게 하는 과정입니다.
특히 여기서 두번째항(=정규항)은 reconstruction을 할 때 아무렇게나 하면안된다는 제약 조건을 주는 것입니다.
마지막항에 대해서는 \(p(z \mid x)\)의 값을 알수 없기 때문에 control 할 수 없습니다.
이점이 VAE의 한계로 지적되는 점입니다.

'Diffusion' 카테고리의 다른 글
| [Diffusion] DDPM에 대해 정리한 내용 (0) | 2025.03.28 |
|---|---|
| [Diffusion] VAE (Variational Autoencoder)에 대한 공부 (0) | 2025.03.27 |
| [Diffusion] Generative Models 2 (GAN/Wasserstein GAN/Pix2pix/CycleGAN (0) | 2025.03.03 |