[Diffusion] DDPM에 대해 정리한 내용

개념 설명을 위해 성민혁 교수님 ppt자료를 수정하여 재작성한 것입니다.

 

앞서 말한 VAE에서 처럼 직접 계산할 수 없기 때문에 하한선(lower bound)을 이용하여 \(log(P_0)\)를 모델링합니다.

여기서 먼저 Consistency term부터 살펴보겠습니다.

Consistency term은 시점 t에 대해 forward step과 reverse step이 동일하게 만드는 것입니다.

하지만 이 경우 보시는 것처럼 2개의 random variables에 대해 계산을 해야 하기 때문에 computaionally 비쌉니다.

 

계산복잡도를 줄이기 위해 random variables이 2개인 상황을 피할 방법을 찾아야 합니다.

그래서 ELBO 식을 Marcov process임을 이용하여 재구성합니다.

다음과 같이 재구성되는데 첫 번째 항 Reconstruction term은 변함이 없고 실제로는 너무 값이 작아 무시된다고 합니다.

두 번째 항은 Prior matching term으로 VAE에서 봤던 term과 동일합니다.

마지막 항은 Denoising matching term입니다. 

 

첫 번째 항부터 보면

\(x_1\) 은 \(x_0\) 의 한 단계 noisy 한 version으로 모델은 쉽게 복원할 수 있다.

 

두 번째 항인 Prior matching term을 보면

두 분포는 학습 전에 predefine 돼 있습니다.

\(P(x_T)\)는 표준정규 분포로 정했고 \(q(x_T|x_0)\)은 어떻게 정의되는지 알아보겠습니다.

앞에서 설명했던 가우시안 noisy를 더하는 과정의 식을 이용하겠습니다.

\(q(x_t|x_{t-1})\)은 다음과 같이 정의하고 계산의 편의를 위해 \(\alpha_t\)를 다음과 같이 \(1-\beta_t\)로 정의하겠습니다.

그럼 \(q(x_t|x_{t-1})\)를 다음과 같이 표현할 수 있습니다.

\(x_0\)일 때 \(x_T\)의 확률은 t-1일 때 t일 일련의 확률을 통해 구할 수 있습니다.

두 가지 개념에 대해 먼저 알아야 하는데

 

첫 번째 개념은 두 개의 가우시안 분포가 있을 때 두 변수의 합에 대해 어떤 분포를 가지는지에 대한 내용입니다.

평균은 각 분포의 평균의 합이고 분산도 동일하게 더해서 구할 수 있습니다.

 

두 번째 개념은 표준정규 분포를 따르는 noise 변수 \(\epsilon\)을 도입하여 정규 분포식을 다시 작성해 주는 것입니다.

따라서 \(x_1\) 이 평균이 \(\sqrt{\alpha_1} \mathbf{x}_0\) 이고 분산이 \(\sqrt{1 - \alpha_1} \)을 따르는 식을 다음과 같이 쓸 수 있습니다.

\(x_0\) 를 이용하여 \(x_2\) 의 분포를 나타내는 방법은 위와 같이 \(x_1\) 에 대입하여 정리합니다.

그럼 다음과 같은 식이 되고

이를 구하고자 하는 time인 t까지 진행했을 때 다음과 같이 됩니다.

T가 무한대로 가는 경우 1보다 작은 값이 계속 곱해지므로 결국 \(\alpha_T\)는 0으로 수렴합니다.

그럼 요 식에 0을 대입하면 결국 \(x_t\)는 표준정규분포를 따름을 알아낼 수 있습니다.

그럼 결국 두 분포가 동일해져 KL-divergence가 0이 됩니다.

Denoising matching term에서 정답인 분포에 대해 살펴보면, 이 분포는 baye's rule을 이용하여 표현을 조금 바꿀 수 있습니다.

밑에 참고용으로 joint distribution에 대한 baye's rule 유도 과정을 넣어놨습니다.

이 ground truth의 분포에 대해 표현하면 다음과 같이 나타낼 수 있고 각 분포는 앞서 정의했던 분포로 표현할 수 있습니다.

정리하면 다음과 같이 되는데

가우시안 분포의 결합은 일반적으로 가우시안 분포를 따르지 않습니다.

그러나 여기서 diffusion model의 특수한 구조로 가우시안 분포를 따른다 했고 정리하면 다음과 같이 표현할 수 있습니다.

여기서 중요한 것은 mean이 \(x_t\)와 \(x_0\) 에 대한 함수라는 것입니다.

그리고 분산은 앞서 정의한 forward process의 계수들로 표현됩니다.

따라서 이는 미리 계산 가능한 상수 값입니다.

따라서 우리는 mean에 대해서만 학습하면 됩니다.

\(X_0\)에 대해 정리해서 mean function에 넣어 mean function을 \(x_t\)와 \(\epsilon_t\)에 대해 정리합니다.

이렇게 정리하는 이유는 \(x_0\)를 예측하는 것 보다 \(\epsilon_t\)를 예측하는 것이 더 성능이 높기 때문입니다.

다시 Denoising matching term으로 돌아와서 variational distribution을 모델링 하고 어떻게 학습이 되어가는지 알아보겠습니다.

아까 보았듯이 ground truth의 분산은 상수 였습니다.

따라서 variational distribution도 분산은 상수로 정해놓고 mean만 학습할 수 있도록 합니다.

 

다음과 같이 noisy sample \(x_t\)와  time step \(t\)에서, 이전 상태의 \(x_{t-1}\)의 평균을 예측하는 predictor를 모델링 합니다.

이를 mean predictor라 합니다.

이제 denoising matching term에 돌아와서 두 분포의 KL-divergence를 어떻게 계산하는지 알아보겠습니다.

분산이 동일한 두 정규 분포의 KL divergence는 두 평균의 차의 제곱으로 표현할 수 있습니다.

여기에 대해서는 자세하게 증명하진 않겠습니다.

따라서, 두 분포는 분산이 동일하므로 ground truth의 mean function과 mean predictor와의 차의 제곱으로 표현할 수있습니다.

더 나아가서 mean predictor가 아닌 \(x_0\)를 바로 예측하는 predictor를 설계하면 어떨까요?

다음과 같이 정리 할수있습니다.

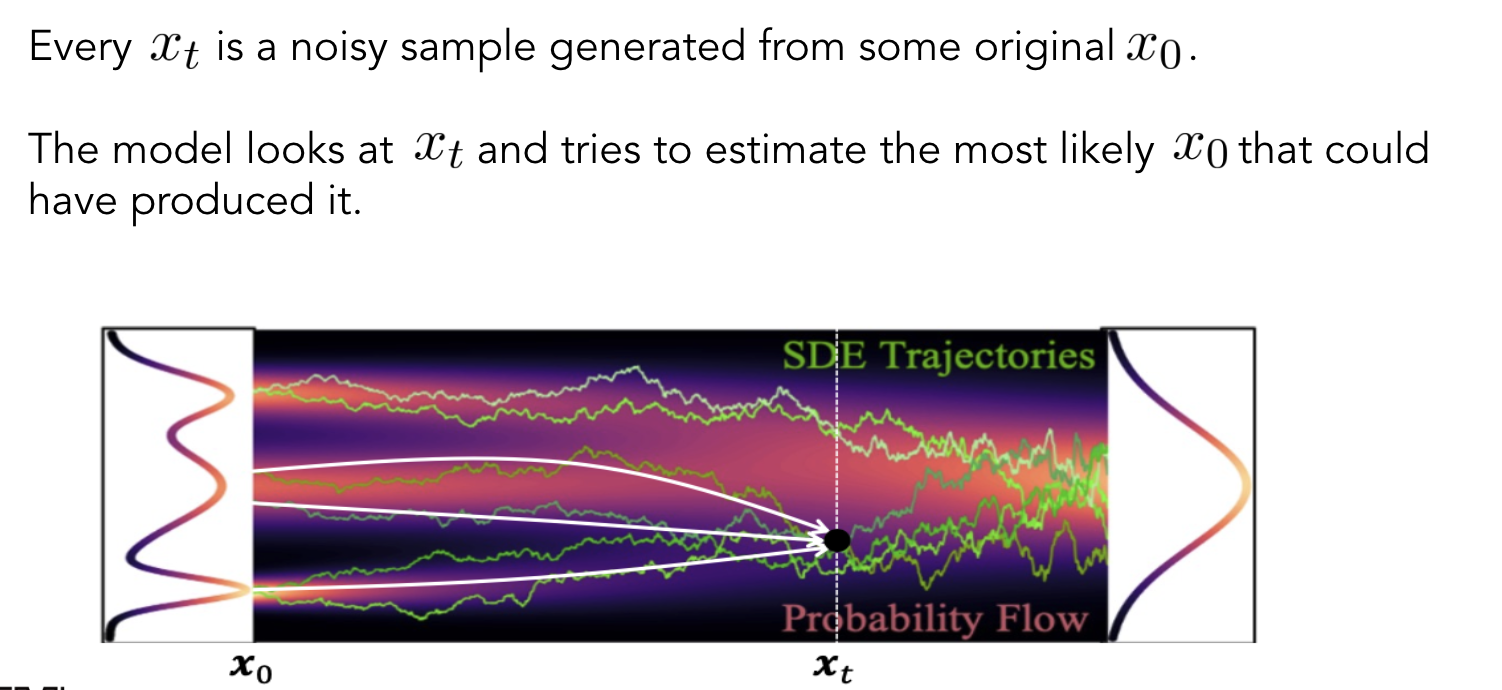
아무래도 평균을 예측하는 것보다 바로 \(x_0\)를 예측하는 것이 더 성능이 좋다고 합니다.

\(x_0\) predictor는 \(x_t\)를 보고 가장 가능성이 있는 \(x_0\)를 구하는 과정입니다.

 

그럼 \(\epsilon_t\)를 예측하는 것은 어떨까요?

실제로 \(\epsilon_t\)를 예측하는 것이 성능이 가장 높다고 합니다.

\(\epsilon_t\)는 표준정규분포이기 때문에 분포와 스케일이 일정하여 안정적으로 학습이 가능합니다.

 

학습은 다음과 같이 시킵니다.

\(x_0\)를 고르고 time step을 균등하게 만듭니다.

3,4번 과정을 통해 noisy를 더한 \(x_t\)를 만듭니다.

이후 \(\epsilon\)predictor를 설계하여 MSE loss를 계산하여 backpropagation을 진행합니다.

 

다음은 generation 과정입니다.

\(x_T\)는 표준정규분포를 따르고 목표는 각 앞단계를 샘플링 하는 것입니다.

이 경우에 1번 계산으로 \(x_t\)에서 \(x_0\)를 복원한뒤, 그것을 다시 3번 계산으로 통해 \(x_{t-1}\)로 돌아옵니다.

이러면 t에서 t-1을 예측한 꼴이됩니다. 이렇게 하는 이유는 무조건 초기 시점으로 가면 noisy 계산을 1번만 해도되서 효율적입니다.

이런식으로 T번 반복하여 generation을 합니다.

결론은 다음과 같습니다.

ELBO식을 전개했을 때 3가지 term으로 구성되지만 첫번째 term은 무시할만큼 작고 두번째 term은 0이 됩니다.

마지막 term에 대해서는 3가지 predictor중 가장 성능이 좋은 \(\epsilon\) predictor를 이용하여 \(\epsilon\)을 예측해 KL-Divergence값을 줄입니다.