[Diffusion] VAE (Variational Autoencoder)에 대한 공부

Diffusion

ysk1m 2025. 3. 27. 19:07

성민혁 교수님 강의를 보고 공부한 내용.

일단 처음 배우면 너무 어지러워서 뭘 배우려하는지, 어떻게 배우려하는지를 중심으로 정리해보았다.

VAE가 구하려하는 것

이미지를 생성하려고 하는데, 그 이미지가 생성될 확률을 구하는 것이다.

즉, VAE는 실제 이미지 \(x\)에 대해 \(P(x)\)를 알아내려하는 것이다.

우리가 설계한 모델이 실제 이미지 \(x\)만큼 얼마나 잘 표현하고 있는지를 보는 것이다.

그럼 \(P(x)\)를 구하는 방법에 대해 알아보자.

먼저, \(Monte-Carlo\) 방법을 이용해서 구할 수있다.

다음과 같이 표현할 수있는데

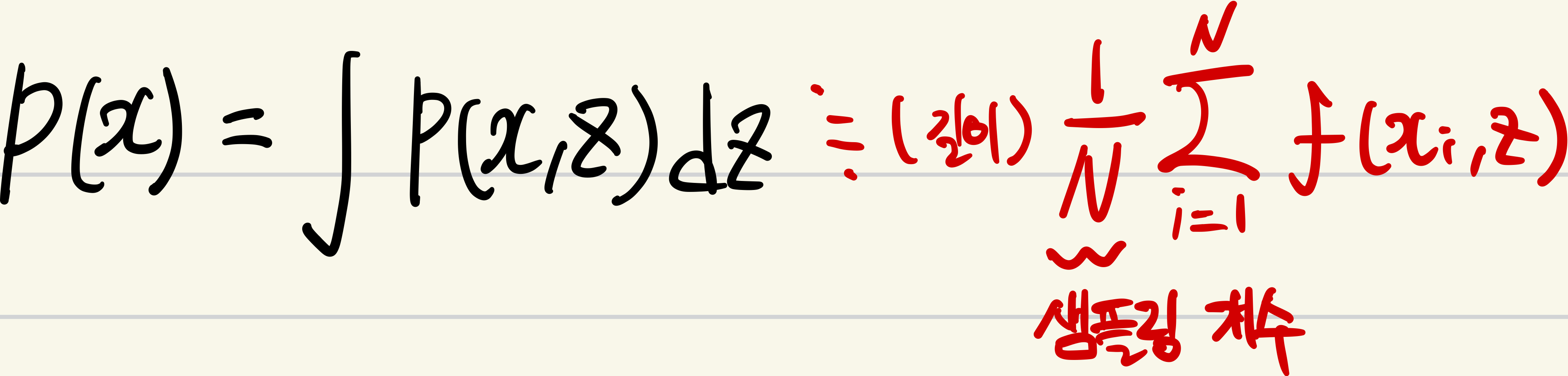
구간에 대해 균등하게 random number를 샘플링해서 적분을 근사하는 것이다.

하지만 정확도를 높이려면 많은 sampling을 해야하는데 그러면 시간이 오래걸려 적절하지 않습니다.

그럼 이 방법말고 다른 방법은 알아봅시다.

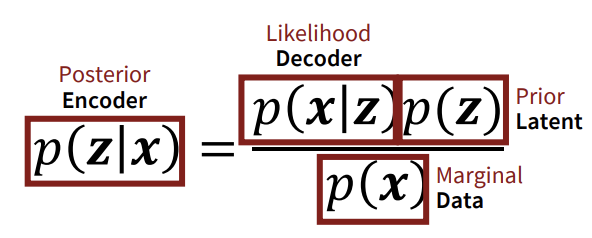
\(P(x)\)를 구하기 위해 Posterior, Likelihood, Prior을 구하면된다..

\(Bayes's rule\)을 이용한 VAE의 큰 구조는 다음과 같다.

직접 구할 수 없어 대부분 가정을 하고 사용하는데

\(P(z)\)(Prior distribution): 주로 표준정규분포로 가정한다.
\(P(z|x)\)(Posterior): Encoder를 통해 입력 \(x\)로 부터 잠재변수 \(z\)를 예측한다. 따라서 \(q_{\phi}(z \mid x) = \mathcal{N}(z ; \mu_{\phi}(x), \sigma_{\phi}^2(x) I)\)으로 근사할 수 있다.
\(P(x|z)\)(Likelihood): Decoder가 잠재 변수 \(z\)로 부터 복원한 값이다.

그럼 이제 다시 돌아와서 \(P(x)\)를 구하는 것이 목표였는데 log likelihood \(log (p(x))\)을 최대화하는 방법을 알아보자.

그러나 직접 최적화하기 어려우므로 ELBO(Evidence Lower Bound)를 이용한다.

직접 유도를 해보았다.

이제 이 \(\mathbb{E}_{q_{\phi}(z \mid x)} \left[ \log \frac{p(x, z)}{q_{\phi}(z \mid x)} \right]\)값을 높이면 되는데

더 정리해보면

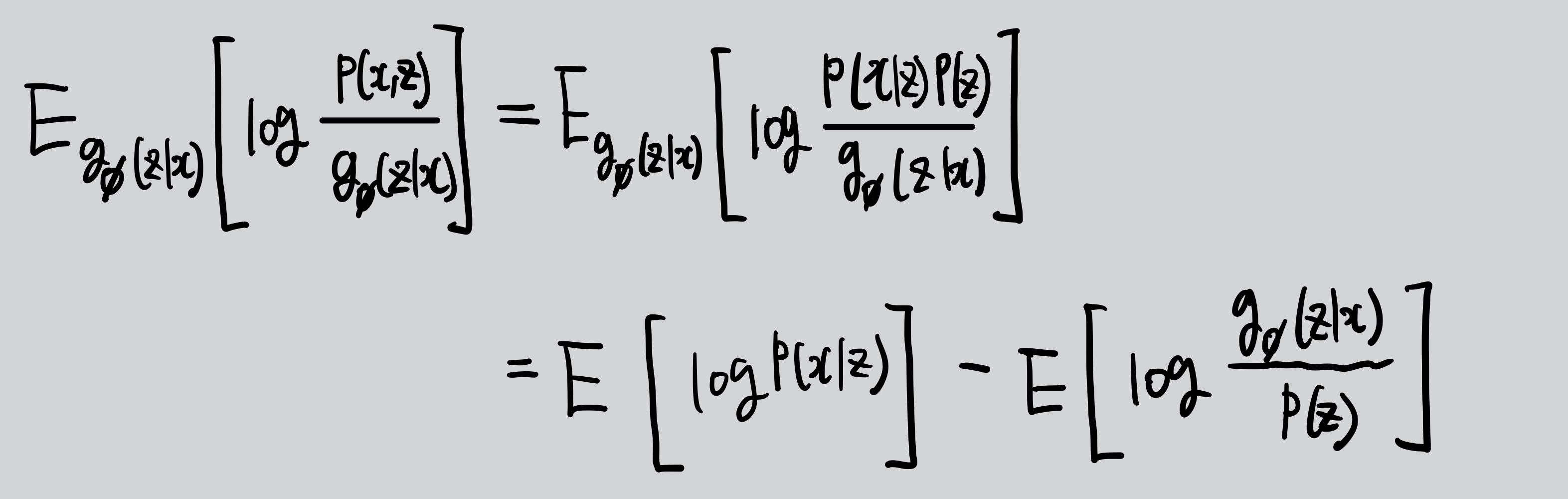
첫 번째 항을 Reconstruction term to be maximized라 하고 두 번째 항을 Prior matching term to be minimized라 한다.

이제 negative ELBO에 gradient decent를 적용하여 train을 한다.

하지만 VAE에도 한계가 있었으니..

VAE로 생성했을 때, 실패했을 경우의 예시이다.

그 이유는 크게 3가지이다.

근사한 Posterior의 한계: 실제 더 복잡한 분포를 단순한 가우시안으로 가정하는 것은 문제가 될 수있다.
ELBO의 한계: 실제 \(log(p(x)\)를 최대화하는게 아닌 하한 값을 최대화하기 때문에 품질에 제한이 있을 수 있다.
실제 이미지 \(x\)의 차원과 latent variable \(z\)의 차원이 다르기 때문에 \(z\)space에 정보를 온전히 전달할 수 없다.